In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.

In geometry, a solid angle is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle at that point.
In Einstein's theory of general relativity, the Schwarzschild metric is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916.
In general relativity, Eddington–Finkelstein coordinates are a pair of coordinate systems for a Schwarzschild geometry which are adapted to radial null geodesics. Null geodesics are the worldlines of photons; radial ones are those that are moving directly towards or away from the central mass. They are named for Arthur Stanley Eddington and David Finkelstein. Although they appear to have inspired the idea, neither ever wrote down these coordinates or the metric in these coordinates. Roger Penrose seems to have been the first to write down the null form but credits it to the above paper by Finkelstein, and, in his Adams Prize essay later that year, to Eddington and Finkelstein. Most influentially, Misner, Thorne and Wheeler, in their book Gravitation, refer to the null coordinates by that name.
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find.
A nonholonomic system in physics and mathematics is a physical system whose state depends on the path taken in order to achieve it. Such a system is described by a set of parameters subject to differential constraints and non-linear constraints, such that when the system evolves along a path in its parameter space but finally returns to the original set of parameter values at the start of the path, the system itself may not have returned to its original state. Nonholonomic mechanics is autonomous division of Newtonian mechanics.
In physics and astronomy, the Reissner–Nordström metric is a static solution to the Einstein–Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M. The analogous solution for a charged, rotating body is given by the Kerr–Newman metric.
In mathematics, a Killing vector field, named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold. More simply, the flow generates a symmetry, in the sense that moving each point of an object the same distance in the direction of the Killing vector will not distort distances on the object.
In general relativity, Schwarzschild geodesics describe the motion of test particles in the gravitational field of a central fixed mass that is, motion in the Schwarzschild metric. Schwarzschild geodesics have been pivotal in the validation of Einstein's theory of general relativity. For example, they provide accurate predictions of the anomalous precession of the planets in the Solar System and of the deflection of light by gravity.
The Kerr–Newman metric is the most general asymptotically flat and stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged and rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions; that is, it is a solution to the Einstein–Maxwell equations that account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions.
The Schwarzschild solution describes spacetime under the influence of a massive, non-rotating, spherically symmetric object. It is considered by some to be one of the simplest and most useful solutions to the Einstein field equations.
In physics, spherically symmetric spacetimes are commonly used to obtain analytic and numerical solutions to Einstein's field equations in the presence of radially moving matter or energy. Because spherically symmetric spacetimes are by definition irrotational, they are not realistic models of black holes in nature. However, their metrics are considerably simpler than those of rotating spacetimes, making them much easier to analyze.
A frame field in general relativity is a set of four pointwise-orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime. The timelike unit vector field is often denoted by and the three spacelike unit vector fields by . All tensorial quantities defined on the manifold can be expressed using the frame field and its dual coframe field.
A theoretical motivation for general relativity, including the motivation for the geodesic equation and the Einstein field equation, can be obtained from special relativity by examining the dynamics of particles in circular orbits about the Earth. A key advantage in examining circular orbits is that it is possible to know the solution of the Einstein Field Equation a priori. This provides a means to inform and verify the formalism.
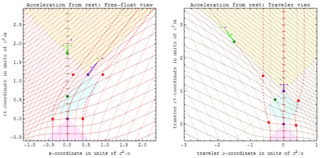
In relativity theory, proper acceleration is the physical acceleration experienced by an object. It is thus acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured. Gravitation therefore does not cause proper acceleration, because the same gravity acts equally on the inertial observer. As a consequence, all inertial observers always have a proper acceleration of zero.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to
In general relativity, the Vaidya metric describes the non-empty external spacetime of a spherically symmetric and nonrotating star which is either emitting or absorbing null dusts. It is named after the Indian physicist Prahalad Chunnilal Vaidya and constitutes the simplest non-static generalization of the non-radiative Schwarzschild solution to Einstein's field equation, and therefore is also called the "radiating(shining) Schwarzschild metric".
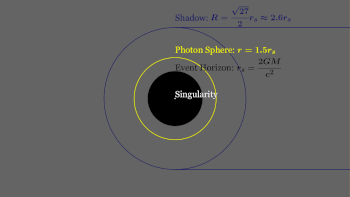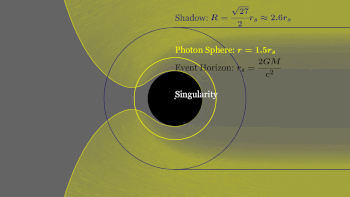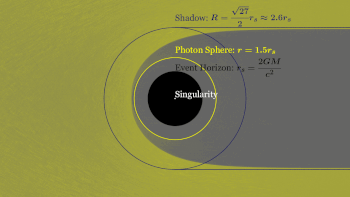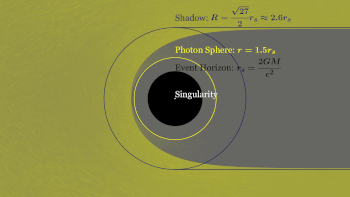
Photon sphere (definition):
A photon sphere of a static spherically symmetric metric is a timelike hypersurface if the deflection angle of a light ray with the closest distance of approach diverges as
In general relativity, the Weyl metrics are a class of static and axisymmetric solutions to Einstein's field equation. Three members in the renowned Kerr–Newman family solutions, namely the Schwarzschild, nonextremal Reissner–Nordström and extremal Reissner–Nordström metrics, can be identified as Weyl-type metrics.
Calculations in the Newman–Penrose (NP) formalism of general relativity normally begin with the construction of a complex null tetrad, where is a pair of real null vectors and is a pair of complex null vectors. These tetrad vectors respect the following normalization and metric conditions assuming the spacetime signature