
Poisson clumping, or Poisson bursts, [1] is a phenomenon where random events may appear to occur in clusters, clumps, or bursts.

Poisson clumping, or Poisson bursts, [1] is a phenomenon where random events may appear to occur in clusters, clumps, or bursts.
Poisson clumping is named for 19th-century French mathematician Siméon Denis Poisson, [1] known for his work on definite integrals, electromagnetic theory, and probability theory, and after whom the Poisson distribution is also named.
The Poisson process provides a description of random independent events occurring with uniform probability through time and/or space. The expected number λ of events in a time interval or area of a given measure is proportional to that measure. The distribution of the number of events follows a Poisson distribution entirely determined by the parameter λ. If λ is small, events are rare, but may nevertheless occur in clumps—referred to as Poisson clumps or bursts—purely by chance. [2] In many cases there is no other cause behind such indefinite groupings besides the nature of randomness following this distribution. [3] However, obviously not all clumping in nature can be explained by this property — for example earthquakes, because of local seismic activity that causes groups of local aftershocks, in this case Weibull distribution is proposed. [4]
Poisson clumping is used to explain marked increases or decreases in the frequency of an event, such as shark attacks, "coincidences", birthdays, heads or tails from coin tosses, and e-mail correspondence. [5] [6]
The poisson clumping heuristic (PCH), published by David Aldous in 1989, [7] is a model for finding first-order approximations over different areas in a large class of stationary probability models. The probability models have a specific monotonicity property with large exclusions. The probability that this will achieve a large value is asymptotically small and is distributed in a Poisson fashion. [8]

In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.

In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.
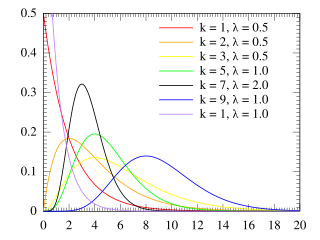
The Erlang distribution is a two-parameter family of continuous probability distributions with support . The two parameters are:

In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It models a broad range of random variables, largely in the nature of a time to failure or time between events. Examples are maximum one-day rainfalls and the time a user spends on a web page.
In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. The result can be either a continuous or a discrete distribution.
A return period, also known as a recurrence interval or repeat interval, is an average time or an estimated average time between events such as earthquakes, floods, landslides, or river discharge flows to occur.
In the field of information retrieval, divergence from randomness, one of the first models, is one type of probabilistic model. It is basically used to test the amount of information carried in the documents. It is based on Harter's 2-Poisson indexing-model. The 2-Poisson model has a hypothesis that the level of the documents is related to a set of documents which contains words occur relatively greater than the rest of the documents. It is not a 'model', but a framework for weighting terms using probabilistic methods, and it has a special relationship for term weighting based on notion of eliteness.
In probability theory, Le Cam's theorem, named after Lucien Le Cam, states the following.
A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.

David John Aldous FRS is a mathematician known for his research on probability theory and its applications, in particular in topics such as exchangeability, weak convergence, Markov chain mixing times, the continuum random tree and stochastic coalescence. He entered St. John's College, Cambridge, in 1970 and received his Ph.D. at the University of Cambridge in 1977 under his advisor, D. J. H. Garling. Aldous was on the faculty at University of California, Berkeley from 1979 until his retirement in 2018.
In probability theory and statistics, the index of dispersion, dispersion index,coefficient of dispersion,relative variance, or variance-to-mean ratio (VMR), like the coefficient of variation, is a normalized measure of the dispersion of a probability distribution: it is a measure used to quantify whether a set of observed occurrences are clustered or dispersed compared to a standard statistical model.

In probability theory and statistics, there are several relationships among probability distributions. These relations can be categorized in the following groups:

For statistics in probability theory, the Boolean-Poisson model or simply Boolean model for a random subset of the plane is one of the simplest and most tractable models in stochastic geometry. Take a Poisson point process of rate in the plane and make each point be the center of a random set; the resulting union of overlapping sets is a realization of the Boolean model . More precisely, the parameters are and a probability distribution on compact sets; for each point of the Poisson point process we pick a set from the distribution, and then define as the union of translated sets.

In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event. It is named after French mathematician Siméon Denis Poisson. The Poisson distribution can also be used for the number of events in other specified interval types such as distance, area, or volume.
Design of robust and reliable networks and network services relies on an understanding of the traffic characteristics of the network. Throughout history, different models of network traffic have been developed and used for evaluating existing and proposed networks and services.
The Borel distribution is a discrete probability distribution, arising in contexts including branching processes and queueing theory. It is named after the French mathematician Émile Borel.

In probability, statistics and related fields, a Poisson point process is a type of random mathematical object that consists of points randomly located on a mathematical space with the essential feature that the points occur independently of one another. The Poisson point process is often called simply the Poisson process, but it is also called a Poisson random measure, Poisson random point field or Poisson point field. This point process has convenient mathematical properties, which has led to its being frequently defined in Euclidean space and used as a mathematical model for seemingly random processes in numerous disciplines such as astronomy, biology, ecology, geology, seismology, physics, economics, image processing, and telecommunications.
A mixed Poisson distribution is a univariate discrete probability distribution in stochastics. It results from assuming that the conditional distribution of a random variable, given the value of the rate parameter, is a Poisson distribution, and that the rate parameter itself is considered as a random variable. Hence it is a special case of a compound probability distribution. Mixed Poisson distributions can be found in actuarial mathematics as a general approach for the distribution of the number of claims and is also examined as an epidemiological model. It should not be confused with compound Poisson distribution or compound Poisson process.