Diagram
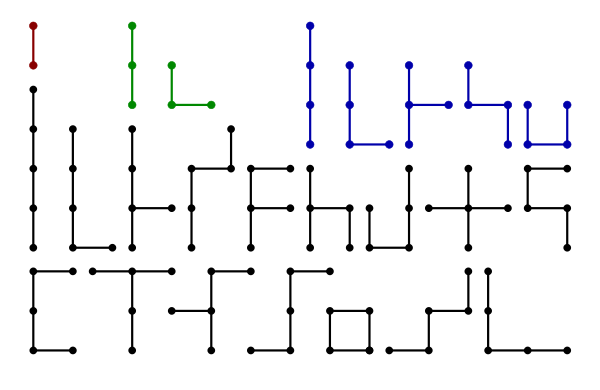
In recreational mathematics, a polystick (or polyedge) is a polyform with a line segment (a 'stick') as the basic shape. A polystick is a connected set of segments in a regular grid. A square polystick is a connected subset of a regular square grid. A triangular polystick is a connected subset of a regular triangular grid. Polysticks are classified according to how many line segments they contain. [1]
The name "polystick" seems to have been first coined by Brian R. Barwell. [2]
The names "polytrig" [3] and "polytwigs" [4] has been proposed by David Goodger to simplify the phrases "triangular-grid polysticks" and "hexagonal-grid polysticks," respectively. Colin F. Brown has used an earlier term "polycules" for the hexagonal-grid polysticks due to their appearance resembling the spicules of sea sponges. [5]
There is no standard term for line segments built on other regular tilings, an unstructured grid, or a simple connected graph, but both "polynema" and "polyedge" have been proposed. [6]
When reflections are considered distinct we have the one-sided polysticks. When rotations and reflections are not considered to be distinct shapes, we have the free polysticks. Thus, for example, there are 7 one-sided square tristicks because two of the five shapes have left and right versions. [7] [8]
Square Polysticks | |||
| Sticks | Name | Free OEIS: A019988 | One-Sided OEIS: A151537 |
|---|---|---|---|
| 1 | monostick | 1 | 1 |
| 2 | distick | 2 | 2 |
| 3 | tristick | 5 | 7 |
| 4 | tetrastick | 16 | 25 |
| 5 | pentastick | 55 | 99 |
| 6 | hexastick | 222 | 416 |
| 7 | heptastick | 950 | 1854 |
Hexagonal Polysticks | |||
| Sticks | Name | Free OEIS: A197459 | One-Sided OEIS: A197460 |
|---|---|---|---|
| 1 | monotwig | 1 | 1 |
| 2 | ditwig | 1 | 1 |
| 3 | tritwigs | 3 | 4 |
| 4 | tetratwigs | 4 | 6 |
| 5 | pentatwigs | 12 | 19 |
| 6 | hexatwigs | 27 | 49 |
| 7 | heptatwigs | 78 | 143 |
Triangular Polysticks | |||
| Sticks | Name | Free OEIS: A159867 | One-Sided OEIS: A151539 |
|---|---|---|---|
| 1 | monostick | 1 | 1 |
| 2 | distick | 3 | 3 |
| 3 | tristick | 12 | 19 |
| 4 | tetrastick | 60 | 104 |
| 5 | pentastick | 375 | 719 |
| 6 | hexastick | 2613 | 5123 |
| 7 | heptastick | 19074 | 37936 |
The set of n-sticks that contain no closed loops is equivalent, with some duplications, to the set of (n+1)-ominos, as each vertex at the end of every line segment can be replaced with a single square of a polyomino. For example, the set of tristicks is equivalent to the set of Tetrominos. In general, an n-stick with m loops is equivalent to a (n−m+1)-omino (as each loop means that one line segment does not add a vertex to the figure).

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.

In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.

In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron or omnitruncated icosahedron is an Archimedean solid, one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces.

In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,4,3}. It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.

In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word diagonal derives from the ancient Greek διαγώνιος diagonios, "from angle to angle" ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a rhombus or cuboid, and later adopted into Latin as diagonus.
In geometry, a zonohedron is a convex polyhedron that is centrally symmetric, every face of which is a polygon that is centrally symmetric. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional projection of a hypercube. Zonohedra were originally defined and studied by E. S. Fedorov, a Russian crystallographer. More generally, in any dimension, the Minkowski sum of line segments forms a polytope known as a zonotope.

Euclidean plane tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in his Harmonices Mundi.

In the mathematical discipline of graph theory, the dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is oblique. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.

In geometry, the hexagonal prism is a prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 faces, 18 edges, and 12 vertices.

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} .

In geometry, the square tiling, square tessellation or square grid is a regular tiling of the Euclidean plane. It has Schläfli symbol of {4,4}, meaning it has 4 squares around every vertex.

In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.

In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.
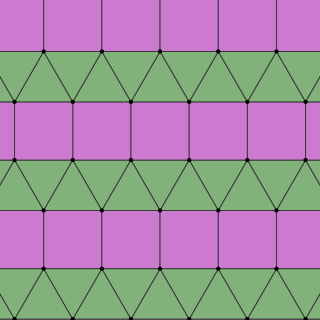
In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.

A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.
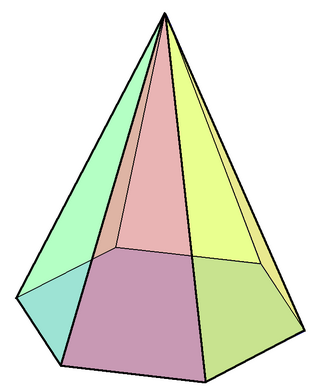
In geometry, a hexagonal pyramid or hexacone is a pyramid with a hexagonal base upon which are erected six isosceles triangular faces that meet at a point. Like any pyramid, it is self-dual.

In geometry, a parallelohedron is a polyhedron that can be translated without rotations in 3-dimensional Euclidean space to fill space with a honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron.

In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of Scientific American. In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in Mathematics Magazine.