Examples
Here are some examples of probability vectors. The vectors can be either columns or rows.
In mathematics and statistics, a probability vector or stochastic vector is a vector with non-negative entries that add up to one.
The positions (indices) of a probability vector represent the possible outcomes of a discrete random variable, and the vector gives us the probability mass function of that random variable, which is the standard way of characterizing a discrete probability distribution. [1]
Here are some examples of probability vectors. The vectors can be either columns or rows.
Writing out the vector components of a vector as
the vector components must sum to one:
Each individual component must have a probability between zero and one:
for all . Therefore, the set of stochastic vectors coincides with the standard -simplex. It is a point if , a segment if , a (filled) triangle if , a (filled) tetrahedron , etc.

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

A random variable is a variable whose values depend on outcomes of a random event. Also called random quantity, aleatory variable, or stochastic variable. It is formally defined as a measurable function. It maps from the sample space to a measurable space on the probability space.
In probability theory, the central limit theorem (CLT) establishes that, in many situations, when independent random variables are summed up, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions. This theorem has seen many changes during the formal development of probability theory. Previous versions of the theorem date back to 1811, but in its modern general form, this fundamental result in probability theory was precisely stated as late as 1920, thereby serving as a bridge between classical and modern probability theory.

In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value.
In probability theory, Chebyshev's inequality guarantees that, for a wide class of probability distributions, no more than a certain fraction of values can be more than a certain distance from the mean. Specifically, no more than 1/k2 of the distribution's values can be k or more standard deviations away from the mean. The rule is often called Chebyshev's theorem, about the range of standard deviations around the mean, in statistics. The inequality has great utility because it can be applied to any probability distribution in which the mean and variance are defined. For example, it can be used to prove the weak law of large numbers.
In mathematics, particularly in linear algebra, a skew-symmetricmatrix is a square matrix whose transpose equals its negative. That is, it satisfies the condition
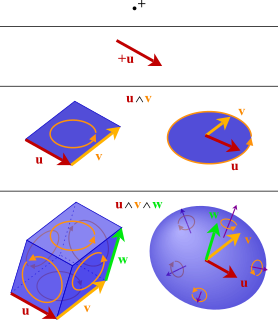
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogues. The exterior product of two vectors and , denoted by , is called a bivector and lives in a space called the exterior square, a vector space that is distinct from the original space of vectors. The magnitude of can be interpreted as the area of the parallelogram with sides and , which in three dimensions can also be computed using the cross product of the two vectors. More generally, all parallel plane surfaces with the same orientation and area have the same bivector as a measure of their oriented area. Like the cross product, the exterior product is anticommutative, meaning that for all vectors and , but, unlike the cross product, the exterior product is associative.

In probability theory and statistics, the Rayleigh distribution is a continuous probability distribution for nonnegative-valued random variables. Up to rescaling, it coincides with the chi distribution with two degrees of freedom.
In quantum field theory, the Dirac spinor is the spinor that describes all known fundamental particles that are fermions, with the possible exception of neutrinos. It appears in the plane-wave solution to the Dirac equation, and is a certain combination of two Weyl spinors, specifically, a bispinor that transforms "spinorially" under the action of the Lorentz group.
In control systems, sliding mode control (SMC) is a nonlinear control method that alters the dynamics of a nonlinear system by applying a discontinuous control signal that forces the system to "slide" along a cross-section of the system's normal behavior. The state-feedback control law is not a continuous function of time. Instead, it can switch from one continuous structure to another based on the current position in the state space. Hence, sliding mode control is a variable structure control method. The multiple control structures are designed so that trajectories always move toward an adjacent region with a different control structure, and so the ultimate trajectory will not exist entirely within one control structure. Instead, it will slide along the boundaries of the control structures. The motion of the system as it slides along these boundaries is called a sliding mode and the geometrical locus consisting of the boundaries is called the sliding (hyper)surface. In the context of modern control theory, any variable structure system, like a system under SMC, may be viewed as a special case of a hybrid dynamical system as the system both flows through a continuous state space but also moves through different discrete control modes.
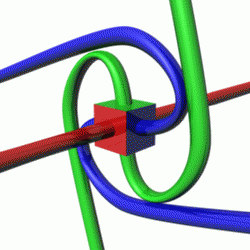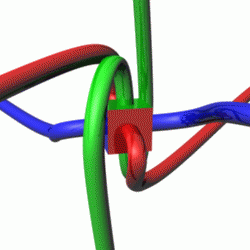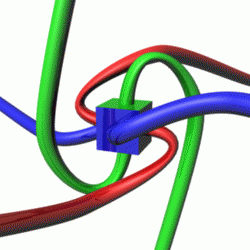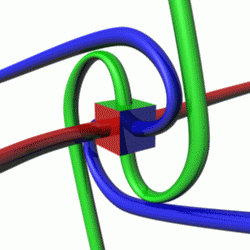
In quantum mechanics, spin is an intrinsic property of all elementary particles. All known fermions, the particles that constitute ordinary matter, have a spin of 1/2. The spin number describes how many symmetrical facets a particle has in one full rotation; a spin of 1/2 means that the particle must be rotated by two full turns before it has the same configuration as when it started.

In continuum mechanics, the Cauchy stress tensor, true stress tensor, or simply called the stress tensor is a second order tensor named after Augustin-Louis Cauchy. The tensor consists of nine components that completely define the state of stress at a point inside a material in the deformed state, placement, or configuration. The tensor relates a unit-length direction vector n to the traction vector T(n) across an imaginary surface perpendicular to n:
In mathematics and physics, in particular quantum information, the term generalized Pauli matrices refers to families of matrices which generalize the properties of the Pauli matrices. Here, a few classes of such matrices are summarized.
A second-order cone program (SOCP) is a convex optimization problem of the form
Stochastic approximation methods are a family of iterative methods typically used for root-finding problems or for optimization problems. The recursive update rules of stochastic approximation methods can be used, among other things, for solving linear systems when the collected data is corrupted by noise, or for approximating extreme values of functions which cannot be computed directly, but only estimated via noisy observations.

In probability theory, a logit-normal distribution is a probability distribution of a random variable whose logit has a normal distribution. If Y is a random variable with a normal distribution, and P is the standard logistic function, then X = P(Y) has a logit-normal distribution; likewise, if X is logit-normally distributed, then Y = logit(X)= log is normally distributed. It is also known as the logistic normal distribution, which often refers to a multinomial logit version (e.g.).
In probability theory, the rectified Gaussian distribution is a modification of the Gaussian distribution when its negative elements are reset to 0. It is essentially a mixture of a discrete distribution and a continuous distribution as a result of censoring.
The unscented transform (UT) is a mathematical function used to estimate the result of applying a given nonlinear transformation to a probability distribution that is characterized only in terms of a finite set of statistics. The most common use of the unscented transform is in the nonlinear projection of mean and covariance estimates in the context of nonlinear extensions of the Kalman filter. Its creator Jeffrey Uhlmann explained that "unscented" was an arbitrary name that he adopted to avoid it being referred to as the “Uhlmann filter.”
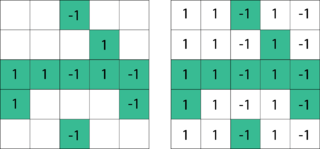
Matrix completion is the task of filling in the missing entries of a partially observed matrix. A wide range of datasets are naturally organized in matrix form. One example is the movie-ratings matrix, as appears in the Netflix problem: Given a ratings matrix in which each entry represents the rating of movie by customer , if customer has watched movie and is otherwise missing, we would like to predict the remaining entries in order to make good recommendations to customers on what to watch next. Another example is the term-document matrix: The frequencies of words used in a collection of documents can be represented as a matrix, where each entry corresponds to the number of times the associated term appears in the indicated document.
The redundancy principle in biology expresses the need of many copies of the same entity to fulfill a biological function. Examples are numerous: disproportionate numbers of spermatozoa during fertilization compared to one egg, large number of neurotransmitters released during neuronal communication compared to the number of receptors, large numbers of released calcium ions during transient in cells and many more in molecular and cellular transduction or gene activation and cell signaling. This redundancy is particularly relevant when the sites of activation is physically separated from the initial position of the molecular messengers. The redundancy is often generated for the purpose of resolving the time constraint of fast-activating pathways. It can be expressed in terms of the theory of extreme statistics to determine its laws and quantify how shortest paths are selected. The main goal is to estimate these large numbers from physical principles and mathematical derivations.