 | This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations .(January 2021) |
A quad-edge data structure is a computer representation of the topology of a two-dimensional or three-dimensional map, that is, a graph drawn on a (closed) surface. It was first described by Jorge Stolfi and Leonidas J. Guibas. [1] It is a variant of the earlier winged edge data structure.
The fundamental idea behind the quad-edge structure is the recognition that a single edge, in a closed polygonal mesh topology, sits between exactly two faces and exactly two vertices.
The quad-edge data structure represents an edge, along with the edges it is connected to around the adjacent vertices and faces to encode the topology of the graph. An example implementation of the quad-edge data-type is as follows
typedefstruct{quadedge_refe[4];}quadedge;typedefstruct{quadedge*next;unsignedintrot;}quadedge_ref;Each quad-edge contains four references to adjacent quad-edges. Each of the four references points to the next edge counter-clockwise around either a vertex or a face. Each of these references represent either the origin vertex of the edge, the right face, the destination vertex, or the left face. Each quad-edge reference points to a quad-edge and the rotation (from 0 to 3) of the 'arm' it points at.
Due to this representation, the quad-edge:
The quad-edge structure gets its name from the general mechanism by which they are stored. A single Edge structure conceptually stores references to up to two faces, two vertices, and 4 edges. The four edges stored are the edges starting with the two vertices that are attached to the two stored faces.
Much like Winged Edge, quad-edge structures are used in programs to store the topology of a 2D or 3D polygonal mesh. The mesh itself does not need to be closed in order to form a valid quad-edge structure.
Using a quad-edge structure, iterating through the topology is quite easy. Often, the interface to quad-edge topologies is through directed edges. This allows the two vertices to have explicit names (start and end), and this gives faces explicit names as well (left and right, relative to a person standing on start and looking in the direction of end). The four edges are also given names, based on the vertices and faces: start-left, start-right, end-left, and end-right. A directed edge can be reversed to generate the edge in the opposite direction.
Iterating around a particular face only requires having a single directed edge to which that face is on the left (by convention) and then walking through all of the start-left edges until the original edge is reached.
In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a general position is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.
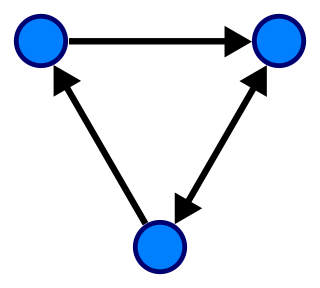
In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.
Breadth-first search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property. It starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next depth level. Extra memory, usually a queue, is needed to keep track of the child nodes that were encountered but not yet explored.
In graph theory and computer science, an adjacency list is a collection of unordered lists used to represent a finite graph. Each unordered list within an adjacency list describes the set of neighbors of a particular vertex in the graph. This is one of several commonly used representations of graphs for use in computer programs.
The point location problem is a fundamental topic of computational geometry. It finds applications in areas that deal with processing geometrical data: computer graphics, geographic information systems (GIS), motion planning, and computer aided design (CAD).
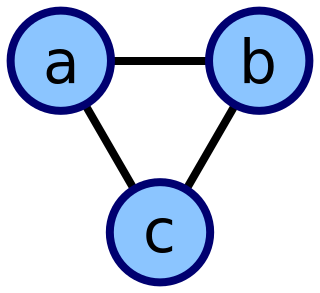
In computer science, a graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from the field of graph theory within mathematics.
In 3D computer graphics and solid modeling, a polygon mesh is a collection of vertices, edges and faces that defines the shape of a polyhedral object. The faces usually consist of triangles, quadrilaterals (quads), or other simple convex polygons (n-gons), since this simplifies rendering, but may also be more generally composed of concave polygons, or even polygons with holes.
In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, they are piecewise-linear Jordan curves consisting of finitely many line segments. They include as special cases the convex polygons, star-shaped polygons, and monotone polygons.
In the field of 3D computer graphics, a subdivision surface is a curved surface represented by the specification of a coarser polygon mesh and produced by a recursive algorithmic method. The curved surface, the underlying inner mesh, can be calculated from the coarse mesh, known as the control cage or outer mesh, as the functional limit of an iterative process of subdividing each polygonal face into smaller faces that better approximate the final underlying curved surface. Less commonly, a simple algorithm is used to add geometry to a mesh by subdividing the faces into smaller ones without changing the overall shape or volume.
In 3D computer graphics, polygonal modeling is an approach for modeling objects by representing or approximating their surfaces using polygon meshes. Polygonal modeling is well suited to scanline rendering and is therefore the method of choice for real-time computer graphics. Alternate methods of representing 3D objects include NURBS surfaces, subdivision surfaces, and equation-based representations used in ray tracers.
In computer graphics, the winged edge data structure is a way to represent polygon meshes in computer memory. It is a type of boundary representation and describes both the geometry and topology of a model. Three types of records are used: vertex records, edge records, and face records. Given a reference to an edge record, one can answer several types of adjacency queries in constant time. This kind of adjacency information is useful for algorithms such as subdivision surface.
In computer graphics, a triangle strip is a subset of triangles in a triangle mesh with shared vertices, and is a more memory-efficient method of storing information about the mesh. They are more efficient than un-indexed lists of triangles, but usually equally fast or slower than indexed triangle lists. The primary reason to use triangle strips is to reduce the amount of data needed to create a series of triangles. The number of vertices stored in memory is reduced from 3N to N + 2, where N is the number of triangles to be drawn. This allows for less use of disk space, as well as making them faster to load into RAM.
In computer graphics, a triangle mesh is a type of polygon mesh. It comprises a set of triangles that are connected by their common edges or vertices.
In computer science, fractional cascading is a technique to speed up a sequence of binary searches for the same value in a sequence of related data structures. The first binary search in the sequence takes a logarithmic amount of time, as is standard for binary searches, but successive searches in the sequence are faster. The original version of fractional cascading, introduced in two papers by Chazelle and Guibas in 1986, combined the idea of cascading, originating in range searching data structures of Lueker (1978) and Willard (1978), with the idea of fractional sampling, which originated in Chazelle (1983). Later authors introduced more complex forms of fractional cascading that allow the data structure to be maintained as the data changes by a sequence of discrete insertion and deletion events.
In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.
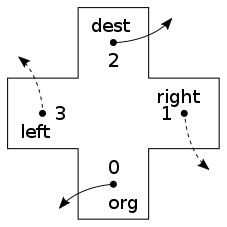
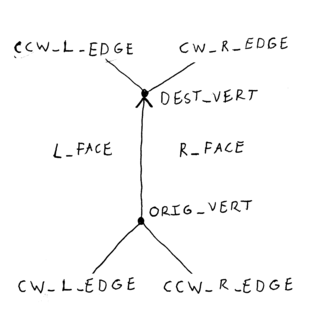
The doubly connected edge list (DCEL), also known as half-edge data structure, is a data structure to represent an embedding of a planar graph in the plane, and polytopes in 3D. This data structure provides efficient manipulation of the topological information associated with the objects in question. It is used in many algorithms of computational geometry to handle polygonal subdivisions of the plane, commonly called planar straight-line graphs (PSLG). For example, a Voronoi diagram is commonly represented by a DCEL inside a bounding box.
In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain is a curve specified by a sequence of points called its vertices. The curve itself consists of the line segments connecting the consecutive vertices.
Leonidas John Guibas is the Paul Pigott Professor of Computer Science and Electrical Engineering at Stanford University. He heads the Geometric Computation group in the Computer Science Department.
In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte (1963), states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.
In solid modeling and computer-aided design, the Euler operators modify the graph of connections to add or remove details of a mesh while preserving its topology. They are named by Baumgart after the Euler–Poincaré characteristic. He chose a set of operators sufficient to create useful meshes, some lose information and so are not invertible.