 | This article needs additional citations for verification .(May 2024) |
A random permutation is a random ordering of a set of objects, that is, a permutation-valued random variable. The use of random permutations is often fundamental to fields that use randomized algorithms such as coding theory, cryptography, and simulation. A good example of a random permutation is the shuffling of a deck of cards: this is ideally a random permutation of the 52 cards.
One method of generating a random permutation of a set of size n uniformly at random (i.e., each of the n! permutations is equally likely to appear) is to generate a sequence by taking a random number between 1 and n sequentially, ensuring that there is no repetition, and interpreting this sequence (x1, ..., xn) as the permutation
shown here in two-line notation.
This brute-force method will require occasional retries whenever the random number picked is a repeat of a number already selected. This can be avoided if, on the ith step (when x1, ..., xi− 1 have already been chosen), one chooses a number j at random between 1 and n−i + 1 and sets xi equal to the jth largest of the unchosen numbers.
A simple algorithm to generate a permutation of n items uniformly at random without retries, known as the Fisher–Yates shuffle, is to start with any permutation (for example, the identity permutation), and then go through the positions 0 through n − 2 (we use a convention where the first element has index 0, and the last element has index n − 1), and for each position iswap the element currently there with a randomly chosen element from positions i through n − 1 (the end), inclusive. It's easy to verify that any permutation of n elements will be produced by this algorithm with probability exactly 1/n!, thus yielding a uniform distribution over all such permutations.
unsigneduniform(unsignedm);/* Returns a random integer 0 <= uniform(m) <= m-1 with uniform distribution */voidinitialize_and_permute(unsignedpermutation[],unsignedn){unsignedi;for(i=0;i<=n-2;i++){unsignedj=i+uniform(n-i);/* A random integer such that i ≤ j < n */swap(permutation[i],permutation[j]);/* Swap the randomly picked element with permutation[i] */}}Note that if the uniform() function is implemented simply as random() % (m) then a bias in the results is introduced if the number of return values of random() is not a multiple of m, but this becomes insignificant if the number of return values of random() is orders of magnitude greater than m.
The probability distribution of the number of fixed points in a uniformly distributed random permutation approaches a Poisson distribution with expected value 1 as n grows. In particular, it is an elegant application of the inclusion–exclusion principle to show that the probability that there are no fixed points approaches 1/e. When n is big enough, the probability distribution of fixed points is almost the Poisson distribution with expected value 1. [1] The first n moments of this distribution are exactly those of the Poisson distribution.
As with all random processes, the quality of the resulting distribution of an implementation of a randomized algorithm such as the Knuth shuffle (i.e., how close it is to the desired uniform distribution) depends on the quality of the underlying source of randomness, such as a pseudorandom number generator. There are many possible randomness tests for random permutations, such as some of the Diehard tests. A typical example of such a test is to take some permutation statistic for which the distribution is known and test whether the distribution of this statistic on a set of randomly generated permutations closely approximates the true distribution.
A hash function is any function that can be used to map data of arbitrary size to fixed-size values, though there are some hash functions that support variable length output. The values returned by a hash function are called hash values, hash codes, hash digests, digests, or simply hashes. The values are usually used to index a fixed-size table called a hash table. Use of a hash function to index a hash table is called hashing or scatter storage addressing.
In mathematics, a permutation of a set can mean one of two different things:
A pseudorandom number generator (PRNG), also known as a deterministic random bit generator (DRBG), is an algorithm for generating a sequence of numbers whose properties approximate the properties of sequences of random numbers. The PRNG-generated sequence is not truly random, because it is completely determined by an initial value, called the PRNG's seed. Although sequences that are closer to truly random can be generated using hardware random number generators, pseudorandom number generators are important in practice for their speed in number generation and their reproducibility.
The Mersenne Twister is a general-purpose pseudorandom number generator (PRNG) developed in 1997 by Makoto Matsumoto and Takuji Nishimura. Its name derives from the choice of a Mersenne prime as its period length.
In computer science, bogosort is a sorting algorithm based on the generate and test paradigm. The function successively generates permutations of its input until it finds one that is sorted. It is not considered useful for sorting, but may be used for educational purposes, to contrast it with more efficient algorithms.
Perlin noise is a type of gradient noise developed by Ken Perlin in 1983. It has many uses, including but not limited to: procedurally generating terrain, applying pseudo-random changes to a variable, and assisting in the creation of image textures. It is most commonly implemented in two, three, or four dimensions, but can be defined for any number of dimensions.
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of N, its subsequence x1, ..., xN has a low discrepancy.
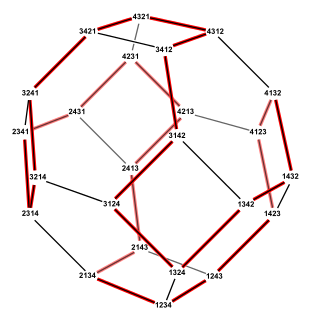
The Steinhaus–Johnson–Trotter algorithm or Johnson–Trotter algorithm, also called plain changes, is an algorithm named after Hugo Steinhaus, Selmer M. Johnson and Hale F. Trotter that generates all of the permutations of elements. Each two adjacent permutations in the resulting sequence differ by swapping two adjacent permuted elements. Equivalently, this algorithm finds a Hamiltonian cycle in the permutohedron, a polytope whose vertices represent permutations and whose edges represent swaps.
Random number generation is a process by which, often by means of a random number generator (RNG), a sequence of numbers or symbols that cannot be reasonably predicted better than by random chance is generated. This means that the particular outcome sequence will contain some patterns detectable in hindsight but impossible to foresee. True random number generators can be hardware random-number generators (HRNGs), wherein each generation is a function of the current value of a physical environment's attribute that is constantly changing in a manner that is practically impossible to model. This would be in contrast to so-called "random number generations" done by pseudorandom number generators (PRNGs), which generate numbers that only look random but are in fact pre-determined—these generations can be reproduced simply by knowing the state of the PRNG.
In computational complexity theory and cryptography, the existence of pseudorandom generators is related to the existence of one-way functions through a number of theorems, collectively referred to as the pseudorandom generator theorem.
In cryptography, a pseudorandom permutation (PRP) is a function that cannot be distinguished from a random permutation (that is, a permutation selected at random with uniform probability, from the family of all permutations on the function's domain) with practical effort.
The ziggurat algorithm is an algorithm for pseudo-random number sampling. Belonging to the class of rejection sampling algorithms, it relies on an underlying source of uniformly-distributed random numbers, typically from a pseudo-random number generator, as well as precomputed tables. The algorithm is used to generate values from a monotonically decreasing probability distribution. It can also be applied to symmetric unimodal distributions, such as the normal distribution, by choosing a value from one half of the distribution and then randomly choosing which half the value is considered to have been drawn from. It was developed by George Marsaglia and others in the 1960s.
A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.
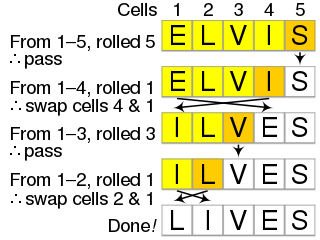
The Fisher–Yates shuffle is an algorithm for shuffling a finite sequence. The algorithm takes a list of all the elements of the sequence, and continually determines the next element in the shuffled sequence by randomly drawing an element from the list until no elements remain. The algorithm produces an unbiased permutation: every permutation is equally likely. The modern version of the algorithm takes time proportional to the number of items being shuffled and shuffles them in place.
In probability theory and statistics, there are several relationships among probability distributions. These relations can be categorized in the following groups:
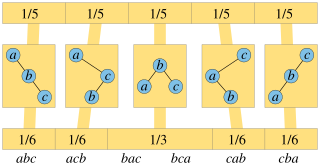
In computer science and probability theory, a random binary tree is a binary tree selected at random from some probability distribution on binary trees. Different distributions have been used, leading to different properties for these trees.
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time if these events occur with a known constant mean rate and independently of the time since the last event. It can also be used for the number of events in other types of intervals than time, and in dimension greater than 1.
Non-uniform random variate generation or pseudo-random number sampling is the numerical practice of generating pseudo-random numbers (PRN) that follow a given probability distribution. Methods are typically based on the availability of a uniformly distributed PRN generator. Computational algorithms are then used to manipulate a single random variate, X, or often several such variates, into a new random variate Y such that these values have the required distribution. The first methods were developed for Monte-Carlo simulations in the Manhattan project, published by John von Neumann in the early 1950s.
In the mathematics of shuffling playing cards, the Gilbert–Shannon–Reeds model is a probability distribution on riffle shuffle permutations. It forms the basis for a recommendation that a deck of cards should be riffled seven times in order to thoroughly randomize it. It is named after the work of Edgar Gilbert, Claude Shannon, and J. Reeds, reported in a 1955 technical report by Gilbert and in a 1981 unpublished manuscript of Reeds.
Birkhoff's algorithm is an algorithm for decomposing a bistochastic matrix into a convex combination of permutation matrices. It was published by Garrett Birkhoff in 1946. It has many applications. One such application is for the problem of fair random assignment: given a randomized allocation of items, Birkhoff's algorithm can decompose it into a lottery on deterministic allocations.