
Epidemiology is the study and analysis of the distribution, patterns and determinants of health and disease conditions in a defined population.
In epidemiology, prevalence is the proportion of a particular population found to be affected by a medical condition at a specific time. It is derived by comparing the number of people found to have the condition with the total number of people studied and is usually expressed as a fraction, a percentage, or the number of cases per 10,000 or 100,000 people. Prevalence is most often used in questionnaire studies.
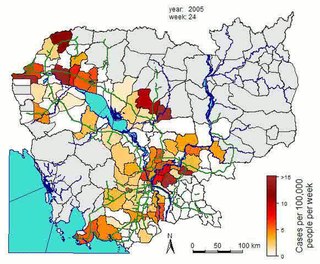
In epidemiology, incidence is a measure of the probability of occurrence of a given medical condition in a population within a specified period of time. Although sometimes loosely expressed simply as the number of new cases during some time period, it is better expressed as a proportion or a rate with a denominator.
The science of epidemiology has matured significantly from the times of Hippocrates, Semmelweis and John Snow. The techniques for gathering and analyzing epidemiological data vary depending on the type of disease being monitored but each study will have overarching similarities.
In survival analysis, the hazard ratio (HR) is the ratio of the hazard rates corresponding to the conditions characterised by two distinct levels of a treatment variable of interest. For example, in a clinical study of a drug, the treated population may die at twice the rate per unit time of the control population. The hazard ratio would be 2, indicating higher hazard of death from the treatment.
An odds ratio (OR) is a statistic that quantifies the strength of the association between two events, A and B. The odds ratio is defined as the ratio of the odds of A in the presence of B and the odds of A in the absence of B, or equivalently, the ratio of the odds of B in the presence of A and the odds of B in the absence of A. Two events are independent if and only if the OR equals 1, i.e., the odds of one event are the same in either the presence or absence of the other event. If the OR is greater than 1, then A and B are associated (correlated) in the sense that, compared to the absence of B, the presence of B raises the odds of A, and symmetrically the presence of A raises the odds of B. Conversely, if the OR is less than 1, then A and B are negatively correlated, and the presence of one event reduces the odds of the other event.
Survival analysis is a branch of statistics for analyzing the expected duration of time until one event occurs, such as death in biological organisms and failure in mechanical systems. This topic is called reliability theory or reliability analysis in engineering, duration analysis or duration modelling in economics, and event history analysis in sociology. Survival analysis attempts to answer certain questions, such as what is the proportion of a population which will survive past a certain time? Of those that survive, at what rate will they die or fail? Can multiple causes of death or failure be taken into account? How do particular circumstances or characteristics increase or decrease the probability of survival?
In statistics, an effect size is a value measuring the strength of the relationship between two variables in a population, or a sample-based estimate of that quantity. It can refer to the value of a statistic calculated from a sample of data, the value of a parameter for a hypothetical population, or to the equation that operationalizes how statistics or parameters lead to the effect size value. Examples of effect sizes include the correlation between two variables, the regression coefficient in a regression, the mean difference, or the risk of a particular event happening. Effect sizes complement statistical hypothesis testing, and play an important role in power analyses, sample size planning, and in meta-analyses. The cluster of data-analysis methods concerning effect sizes is referred to as estimation statistics.

In finance, the duration of a financial asset that consists of fixed cash flows, such as a bond, is the weighted average of the times until those fixed cash flows are received. When the price of an asset is considered as a function of yield, duration also measures the price sensitivity to yield, the rate of change of price with respect to yield, or the percentage change in price for a parallel shift in yields.
In healthcare, a differential diagnosis (DDx) is a method of analysis of a patient's history and physical examination to arrive at the correct diagnosis. It involves distinguishing a particular disease or condition from others that present with similar clinical features. Differential diagnostic procedures are used by clinicians to diagnose the specific disease in a patient, or, at least, to consider any imminently life-threatening conditions. Often, each individual option of a possible disease is called a differential diagnosis.

The positive and negative predictive values are the proportions of positive and negative results in statistics and diagnostic tests that are true positive and true negative results, respectively. The PPV and NPV describe the performance of a diagnostic test or other statistical measure. A high result can be interpreted as indicating the accuracy of such a statistic. The PPV and NPV are not intrinsic to the test ; they depend also on the prevalence. Both PPV and NPV can be derived using Bayes' theorem.

The relative risk (RR) or risk ratio is the ratio of the probability of an outcome in an exposed group to the probability of an outcome in an unexposed group. Together with risk difference and odds ratio, relative risk measures the association between the exposure and the outcome.
In epidemiology, case fatality rate (CFR) – or sometimes more accurately case-fatality risk – is the proportion of people diagnosed with a certain disease, who end up dying of it. Unlike a disease's mortality rate, the CFR does not take into account the time period between disease onset and death. A CFR is generally expressed as a percentage. It represents a measure of disease lethality and may change with different treatments. CFRs are most often used for with discrete, limited-time courses, such as acute infections.
In epidemiology, the attack rate is the proportion of an at-risk population that contracts the disease during a specified time interval. It is used in hypothetical predictions and during actual outbreaks of disease. An at-risk population is defined as one that has no immunity to the attacking pathogen, which can be either a novel pathogen or an established pathogen. It is used to project the number of infections to expect during an epidemic. This aids in marshalling resources for delivery of medical care as well as production of vaccines and/or anti-viral and anti-bacterial medicines.

The risk difference (RD), excess risk, or attributable risk is the difference between the risk of an outcome in the exposed group and the unexposed group. It is computed as , where is the incidence in the exposed group, and is the incidence in the unexposed group. If the risk of an outcome is increased by the exposure, the term absolute risk increase (ARI) is used, and computed as . Equivalently, if the risk of an outcome is decreased by the exposure, the term absolute risk reduction (ARR) is used, and computed as .
Population impact measures (PIMs) are biostatistical measures of risk and benefit used in epidemiological and public health research. They are used to describe the impact of health risks and benefits in a population, to inform health policy.

In medical testing with binary classification, the diagnostic odds ratio (DOR) is a measure of the effectiveness of a diagnostic test. It is defined as the ratio of the odds of the test being positive if the subject has a disease relative to the odds of the test being positive if the subject does not have the disease.
Kermack–McKendrick theory is a hypothesis that predicts the number and distribution of cases of an infectious disease as it is transmitted through a population over time. Building on the research of Ronald Ross and Hilda Hudson, A. G. McKendrick and W. O. Kermack published their theory in a set of three articles from 1927, 1932, and 1933. While Kermack–McKendrick theory was indeed the source of SIR models and their relatives, Kermack and McKendrick were thinking of a more subtle and empirically useful problem than the simple compartmental models discussed here. The text is somewhat difficult to read, compared to modern papers, but the important feature is it was a model where the age-of-infection affected the transmission and removal rates.
An infection rate is the probability or risk of an infection in a population. It is used to measure the frequency of occurrence of new instances of infection within a population during a specific time period.

In epidemiology, attributable fraction for the population (AFp) is the proportion of incidents in the population that are attributable to the risk factor. The term attributable risk percent for the population is used if the fraction is expressed as a percentage. It is calculated as , where is the incidence in the population, and is the incidence in the unexposed group.








