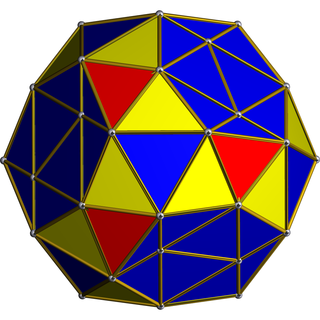
Rectified 600-cell

Last updated
Rectified 600-cell
Rectified 600-cell schlegel halfsolid.png
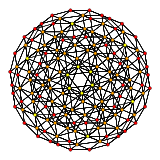
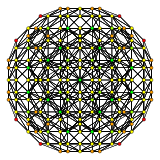
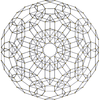
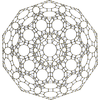
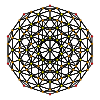
Schlegel diagram, shown as Birectified 120-cell, with 119 icosahedral cells colored
Type Uniform 4-polytope
Uniform index34
Schläfli symbol t1{3,3,5}
or r{3,3,5}
Coxeter-Dynkin diagram CDel node.pngCDel 5.pngCDel node.pngCDel 3.pngCDel node 1.pngCDel 3.pngCDel node.png
Cells600 (3.3.3.3) Uniform polyhedron-33-t1.png
120 {3,5} Icosahedron.png
Faces1200+2400 {3}
Edges3600
Vertices720
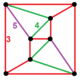
Vertex figure 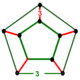Rectified 600-cell verf.png
pentagonal prism
Symmetry group H4, [3,3,5], order 14400
Properties convex, vertex-transitive, edge-transitive

In geometry, the rectified 600-cell or rectified hexacosichoron is a convex uniform 4-polytope composed of 600 regular octahedra and 120 icosahedra cells. Each edge has two octahedra and one icosahedron. Each vertex has five octahedra and two icosahedra. In total it has 3600 triangle faces, 3600 edges, and 720 vertices.

Geometry Branch of mathematics that studies the shape, size and position of objects

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.

Rectification (geometry) process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points

In Euclidean geometry, rectification or complete-truncation is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope.

600-cell four-dimensional analog of the icosahedron

In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,5}. It is also called a C600, hexacosichoron and hexacosihedroid.

Contents

Containing the cell realms of both the regular 120-cell and the regular 600-cell, it can be considered analogous to the polyhedron icosidodecahedron, which is a rectified icosahedron and rectified dodecahedron.

120-cell four-dimensional analog of the dodecahedron

In geometry, the 120-cell is the convex regular 4-polytope with Schläfli symbol {5,3,3}. It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, hecatonicosachoron, dodecacontachoron and hecatonicosahedroid.

Icosidodecahedron Archimedean solid

In geometry, an icosidodecahedron is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.

Icosahedron Polyhedron with 20 faces

In geometry, an icosahedron is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi), meaning 'twenty', and ἕδρα (hédra), meaning 'seat'. The plural can be either "icosahedra" or "icosahedrons".

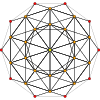
The vertex figure of the rectified 600-cell is a uniform pentagonal prism.

Vertex figure figure exposed when a corner of a polyhedron or polytope is sliced off

In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.

Pentagonal prism prism with a pentagonal base

In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.

Semiregular polytope

It is one of three semiregular 4-polytopes made of two or more cells which are Platonic solids, discovered by Thorold Gosset in his 1900 paper. He called it a octicosahedric for being made of octahedron and icosahedron cells.

In three-dimensional space, a Platonic solid is a regular, convex polyhedron. It is constructed by congruent regular polygonal faces with the same number of faces meeting at each vertex. Five solids meet these criteria:

John Herbert de Paz Thorold Gosset was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher.

Octahedron Polyhedron with 8 faces

In geometry, an octahedron is a polyhedron with eight faces, twelve edges, and six vertices. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as tC600.

Emanuel Lodewijk Elte was a Dutch mathematician. He is noted for discovering and classifying semiregular polytopes in dimensions four and higher.

Alternate names

Polytetrahedron is a term used for three distinct types of objects, all based on the tetrahedron:

Images

Orthographic projections by Coxeter planes
H4-F4
600-cell t1 H4.svg
[30]		 600-cell t1 p20.svg
[20]		 600-cell t1 F4.svg
[12]
H3A2 / B3 / D4A3 / B2
600-cell t1 H3.svg
[10]		 600-cell t1 A2.svg
[6]		 600-cell t1.svg
[4]
Stereographic projection Net
Stereographic rectified 600-cell.png Rectified hexacosichoron net.png

Diminished rectified 600-cell

120-diminished rectified 600-cell
Type4-polytope
Cells840 cells:
600 square pyramid
120 pentagonal prism
120 pentagonal antiprism
Faces2640:
1800 {3}
600 {4}
240 {5}
Edges2400
Vertices600
Vertex figure Spidrox-vertex figure.png
Bi-diminished pentagonal prism
(1) 3.3.3.3 + (4) 3.3.4 Square pyramid.png
(2) 4.4.5 Pentagonal prism.png
(2) 3.3.3.5 Pentagonal antiprism.png
Symmetry group 1/12[3,3,5], order 1200
Properties convex

A related vertex-transitive polytope can be constructed with equal edge lengths removes 120 vertices from the rectified 600-cell, but isn't uniform because it contains square pyramid cells, [1] discovered by George Olshevsky, calling it a swirlprismatodiminished rectified hexacosichoron, with 840 cells (600 square pyramids, 120 pentagonal prisms, and 120 pentagonal antiprisms), 2640 faces (1800 triangles, 600 square, and 240 pentagons), 2400 edges, and 600 vertices. It has a chiral bi-diminished pentagonal prism vertex figure.

Each removed vertex creates a pentagonal prism cell, and diminishes two neighboring icosahedra into pentagonal antiprisms, and each octahedron into a square pyramid. [2]

This polytope can be partitioned into 12 rings of alternating 10 pentagonal prisms and 10 antiprisms, and 30 rings of square pyramids.

Schlegel diagram Orthogonal projection
Spidrox-ring2-perspective.png
Two orthogonal rings shown		 Spidrox-square pyramid ring.png
2 rings of 30 red square pyramids, one ring along perimeter, and one centered.

Swirlprismatodiminished rectified hexacosichoron net.png
Net

H4 family

Pentagonal prism vertex figures

r{p,3,5}
Space S3 H3
FormFiniteCompactParacompactNoncompact
Name r{3,3,5}
CDel node.pngCDel 3.pngCDel node 1.pngCDel 3.pngCDel node.pngCDel 5.pngCDel node.png		 r{4,3,5}
CDel node.pngCDel 4.pngCDel node 1.pngCDel 3.pngCDel node.pngCDel 5.pngCDel node.png
CDel nodes 11.pngCDel split2.pngCDel node.pngCDel 5.pngCDel node.png		 r{5,3,5}
CDel node.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.pngCDel 5.pngCDel node.png		 r{6,3,5}
CDel node.pngCDel 6.pngCDel node 1.pngCDel 3.pngCDel node.pngCDel 5.pngCDel node.png
CDel branch 11.pngCDel split2.pngCDel node.pngCDel 5.pngCDel node.png		r{7,3,5}
CDel node.pngCDel 7.pngCDel node 1.pngCDel 3.pngCDel node.pngCDel 5.pngCDel node.png		... r{∞,3,5}
CDel node.pngCDel infin.pngCDel node 1.pngCDel 3.pngCDel node.pngCDel 5.pngCDel node.png
CDel labelinfin.pngCDel branch 11.pngCDel split2.pngCDel node.pngCDel 5.pngCDel node.png
Image Stereographic rectified 600-cell.png H3 435 CC center 0100.png H3 535 CC center 0100.png H3 635 boundary 0100.png
Cells
Icosahedron.png
{3,5}
CDel node 1.pngCDel 3.pngCDel node.pngCDel 5.pngCDel node.png		 Uniform polyhedron-33-t1.png
r{3,3}
CDel node.pngCDel 3.pngCDel node 1.pngCDel 3.pngCDel node.png		 Cuboctahedron.png
r{4,3}
CDel node.pngCDel 4.pngCDel node 1.pngCDel 3.pngCDel node.png		 Icosidodecahedron.png
r{5,3}
CDel node.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.png		 Uniform tiling 63-t1.svg
r{6,3}
CDel node.pngCDel 6.pngCDel node 1.pngCDel 3.pngCDel node.png		 Triheptagonal tiling.svg
r{7,3}
CDel node.pngCDel 7.pngCDel node 1.pngCDel 3.pngCDel node.png		 H2 tiling 23i-2.png
r{∞,3}
CDel node.pngCDel infin.pngCDel node 1.pngCDel 3.pngCDel node.png

Related Research Articles

4-polytope four-dimensional polytope

In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells.

The term semiregular polyhedron is used variously by different authors.

Uniform 4-polytope 4-polytope which has uniform polyhedra as cells and is vertex-transitive

In geometry, a uniform 4-polytope is a 4-polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.

Runcinated 5-cell

In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

Rectified 5-cell uniform polychoron

In four-dimensional geometry, the rectified 5-cell is a uniform 4-polytope composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10 vertices. Each vertex is surrounded by 3 octahedra and 2 tetrahedra; the vertex figure is a triangular prism.

Snub 24-cell

In geometry, the snub 24-cell or snub disicositetrachoron is a convex uniform 4-polytope composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.

Cubic honeycomb

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway calls this honeycomb a cubille.

Order-5 cubic honeycomb

The order-5 cubic honeycomb is one of four compact regular space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {4,3,5}, it has five cubes {4,3} around each edge, and 20 cubes around each vertex. It is dual with the order-4 dodecahedral honeycomb.

Icosahedral honeycomb

The icosahedral honeycomb is one of four compact regular space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {3,5,3}, there are three icosahedra, {3,5}, around each edge, and 12 icosahedra around each vertex, in a regular dodecahedral, {5,3}, vertex figure.

Grand antiprism Mathematics

In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform 4-polytope bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform 4-polytope, discovered in 1965 by Conway and Guy.

Rectified 120-cell

In geometry, a rectified 120-cell is a uniform 4-polytope formed as the rectification of the regular 120-cell.

Truncated 120-cells

In geometry, a truncated 120-cell is a uniform 4-polytope formed as the truncation of the regular 120-cell.

Cantellated 120-cell

In four-dimensional geometry, a cantellated 120-cell is a convex uniform 4-polytope, being a cantellation of the regular 120-cell.

Runcinated 120-cells

In four-dimensional geometry, a runcinated 120-cell is a convex uniform 4-polytope, being a runcination of the regular 120-cell.

Uniform polytope vertex-transitive polytope bounded by uniform facets

A uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. The uniform polytopes in two dimensions are the regular polygons.

In 4-dimensional geometry, a truncated octahedral prism or omnitruncated tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 16 cells It has 64 faces, and 96 edges and 48 vertices.

Order-4 octahedral honeycomb

In the geometry of hyperbolic 3-space, the order-4 octahedral honeycomb is a regular paracompact honeycomb. It is called paracompact because it has infinite vertex figures, with all vertices as ideal points at infinity. Given by Schläfli symbol {3,4,4}, it has four octahedra, {3,4} around each edge, and infinite octahedra around each vertex in a square tiling {4,4} vertex arrangement.

References

  1. ↑ Category S4: Scaliform Swirlprisms spidrox
  2. ↑ Klitzing, Richard. "4D convex scaliform polychora swirlprismatodiminished rectified hexacosachoron".
Fundamental convex regular and uniform polytopes in dimensions 2–10
Family An Bn I2(p) / Dn E6 / E7 / E8 / F4 / G2 Hn
Regular polygon Triangle Square p-gon Hexagon Pentagon
Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron
Uniform 4-polytope 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell
Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube
Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221
Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321
Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421
Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube
Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube
Uniform n-polytope n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.