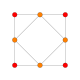
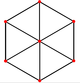
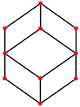
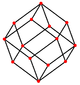
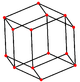
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.
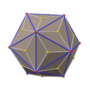
In geometry, an icosidodecahedron is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

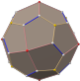
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square, it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.
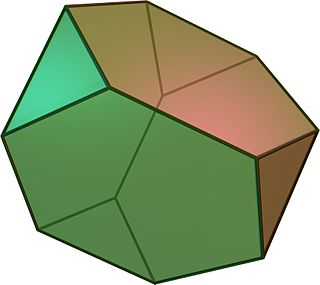
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges. It can be constructed by truncating all 4 vertices of a regular tetrahedron at one third of the original edge length.

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces, 36 edges, and 24 vertices.

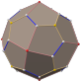
In geometry, the truncated cuboctahedron or great rhombicuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

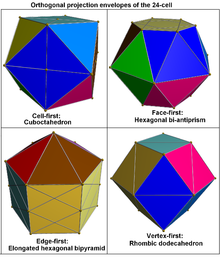
In four-dimensional geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,4,3}. It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.

In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.

In four-dimensional geometry, a cantellated tesseract is a convex uniform 4-polytope, being a cantellation of the regular tesseract.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids.

In the field of hyperbolic geometry, the order-4 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.

In the geometry of hyperbolic 3-space, the square tiling honeycomb is one of 11 paracompact regular honeycombs. It is called paracompact because it has infinite cells, whose vertices exist on horospheres and converge to a single ideal point at infinity. Given by Schläfli symbol {4,4,3}, it has three square tilings, {4,4}, around each edge, and six square tilings around each vertex, in a cubic {4,3} vertex figure.

The skeleton of a cuboctahedron, considering its edges as rigid beams connected at flexible joints at its vertices but omitting its faces, does not have structural rigidity and consequently its vertices can be repositioned by folding at edges and face diagonals. The cuboctahedron's kinematics is noteworthy in that its vertices can be repositioned to the vertex positions of the regular icosahedron, the Jessen's icosahedron, and the regular octahedron, in accordance with the pyritohedral symmetry of the icosahedron.