In geometry, a spherical polyhedron or spherical tiling is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons . A polyhedron whose vertices are equidistant from its center can be conveniently studied by projecting its edges onto the sphere to obtain a corresponding spherical polyhedron.
Contents
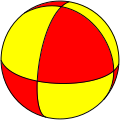
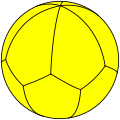
The most familiar spherical polyhedron is the soccer ball, thought of as a spherical truncated icosahedron. The next most popular spherical polyhedron is the beach ball, thought of as a hosohedron.
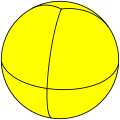
Some "improper" polyhedra, such as hosohedra and their duals, dihedra, exist as spherical polyhedra, but their flat-faced analogs are degenerate. The example hexagonal beach ball, {2, 6}, is a hosohedron, and {6, 2} is its dual dihedron.