In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies of an n-sided polygon, connected by an alternating band of 2n triangles. They are represented by the Conway notation An.
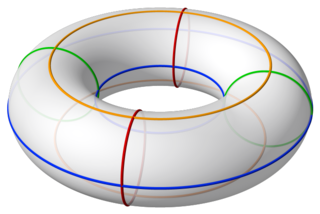
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.

In four-dimensional geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,4,3}. It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.
In geometry, the Dehn invariant is a value used to determine whether one polyhedron can be cut into pieces and reassembled ("dissected") into another, and whether a polyhedron or its dissections can tile space. It is named after Max Dehn, who used it to solve Hilbert's third problem by proving that certain polyhedra with equal volume cannot be dissected into each other.

A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. For each wallpaper there corresponds a group of congruent transformations, with function composition as the group operation. Thus, a wallpaper group is a mathematical classification of a two‑dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tessellations, tiles and physical wallpaper.

The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body with respect to a fixed coordinate system.

In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,5}. It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from "tetrahedral complex") and a polytetrahedron, being bounded by tetrahedral cells.
In mathematics, Hurwitz's automorphisms theorem bounds the order of the group of automorphisms, via orientation-preserving conformal mappings, of a compact Riemann surface of genus g > 1, stating that the number of such automorphisms cannot exceed 84(g − 1). A group for which the maximum is achieved is called a Hurwitz group, and the corresponding Riemann surface a Hurwitz surface. Because compact Riemann surfaces are synonymous with non-singular complex projective algebraic curves, a Hurwitz surface can also be called a Hurwitz curve. The theorem is named after Adolf Hurwitz, who proved it in (Hurwitz 1893).

In geometry, a Schwarz triangle, named after Hermann Schwarz, is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in Schwarz (1873).
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle. Each triangle group is the symmetry group of a tiling of the Euclidean plane, the sphere, or the hyperbolic plane by congruent triangles called Möbius triangles, each one a fundamental domain for the action.
In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO(4). The name comes from the fact that it is the special orthogonal group of order 4.
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.

In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing a Coxeter group or sometimes a uniform polytope or uniform tiling constructed from the group.

In mathematics, the axis–angle representation parameterizes a rotation in a three-dimensional Euclidean space by two quantities: a unit vector e indicating the direction (geometry) of an axis of rotation, and an angle of rotation θ describing the magnitude and sense of the rotation about the axis. Only two numbers, not three, are needed to define the direction of a unit vector e rooted at the origin because the magnitude of e is constrained. For example, the elevation and azimuth angles of e suffice to locate it in any particular Cartesian coordinate frame.
In geometry, pinwheel tilings are non-periodic tilings defined by Charles Radin and based on a construction due to John Conway. They are the first known non-periodic tilings to each have the property that their tiles appear in infinitely many orientations.
In mathematics, a symmetry operation is a geometric transformation of an object that leaves the object looking the same after it has been carried out. For example, a 1⁄3 turn rotation of a regular triangle about its center, a reflection of a square across its diagonal, a translation of the Euclidean plane, or a point reflection of a sphere through its center are all symmetry operations. Each symmetry operation is performed with respect to some symmetry element.
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group (2,3,7) is particularly important for its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84(g − 1), of its automorphism group.

In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson.
Charles Lewis Radin is an American mathematician, known for his work on aperiodic tilings and in particular for defining the pinwheel tiling and, with John Horton Conway, the quaquaversal tiling.

In plane geometry, the einstein problem asks about the existence of a single prototile that by itself forms an aperiodic set of prototiles; that is, a shape that can tessellate space but only in a nonperiodic way. Such a shape is called an einstein, a word play on ein Stein, German for "one stone".