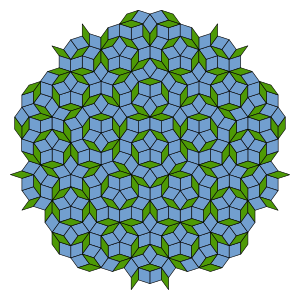
In mathematics, a prototile is one of the shapes of a tile in a tessellation. [1]

In mathematics, a prototile is one of the shapes of a tile in a tessellation. [1]
A tessellation of the plane or of any other space is a cover of the space by closed shapes, called tiles, that have disjoint interiors. Some of the tiles may be congruent to one or more others. If S is the set of tiles in a tessellation, a set R of shapes is called a set of prototiles if no two shapes in R are congruent to each other, and every tile in S is congruent to one of the shapes in R. [2]
It is possible to choose many different sets of prototiles for a tiling: translating or rotating any one of the prototiles produces another valid set of prototiles. However, every set of prototiles has the same cardinality, so the number of prototiles is well defined. A tessellation is said to be monohedral if it has exactly one prototile.

A set of prototiles is said to be aperiodic if every tiling with those prototiles is an aperiodic tiling. In March 2023, four researchers, Chaim Goodman-Strauss, David Smith, Joseph Samuel Myers and Craig S. Kaplan, announced the discovery of an aperiodic monohedral prototile (monotile) and a proof that the tile discovered by David Smith is an aperiodic monotile, i.e. a solution to a longstanding open einstein problem. [3] [4]
In higher dimensions, the problem had been solved earlier: the Schmitt-Conway-Danzer tile is the prototile of a monohedral aperiodic tiling of three-dimensional Euclidean space, and cannot tile space periodically.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.

An aperiodic tiling is a non-periodic tiling with the additional property that it does not contain arbitrarily large periodic regions or patches. A set of tile-types is aperiodic if copies of these tiles can form only non-periodic tilings.

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} .

In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.
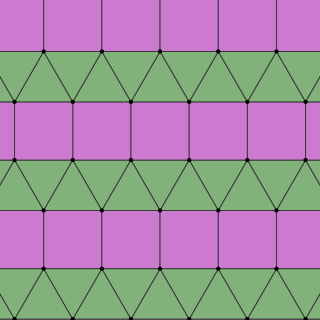
In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.

In geometry, the rhombille tiling, also known as tumbling blocks, reversible cubes, or the dice lattice, is a tessellation of identical 60° rhombi on the Euclidean plane. Each rhombus has two 60° and two 120° angles; rhombi with this shape are sometimes also called diamonds. Sets of three rhombi meet at their 120° angles, and sets of six rhombi meet at their 60° angles.

In geometry, a pentagonal tiling is a tiling of the plane where each individual piece is in the shape of a pentagon.
In geometry, a tile substitution is a method for constructing highly ordered tilings. Most importantly, some tile substitutions generate aperiodic tilings, which are tilings whose prototiles do not admit any tiling with translational symmetry. The most famous of these are the Penrose tilings. Substitution tilings are special cases of finite subdivision rules, which do not require the tiles to be geometrically rigid.

In geometry, a tessellation of dimension 2 or higher, or a polytope of dimension 3 or higher, is isohedral or face-transitive if all its faces are the same. More specifically, all faces must be not merely congruent but must be transitive, i.e. must lie within the same symmetry orbit. In other words, for any two faces A and B, there must be a symmetry of the entire figure by translations, rotations, and/or reflections that maps A onto B. For this reason, convex isohedral polyhedra are the shapes that will make fair dice.

In geometry, a shape is said to be anisohedral if it admits a tiling, but no such tiling is isohedral (tile-transitive); that is, in any tiling by that shape there are two tiles that are not equivalent under any symmetry of the tiling. A tiling by an anisohedral tile is referred to as an anisohedral tiling.

A set of prototiles is aperiodic if copies of the prototiles can be assembled to create tilings, such that all possible tessellation patterns are non-periodic. The aperiodicity referred to is a property of the particular set of prototiles; the various resulting tilings themselves are just non-periodic.

In the mathematical theory of tessellations, the Conway criterion, named for the English mathematician John Horton Conway, is a sufficient rule for when a prototile will tile the plane. It consists of the following requirements: The tile must be a closed topological disk with six consecutive points A, B, C, D, E, and F on the boundary such that:

In plane geometry, the einstein problem asks about the existence of a single prototile that by itself forms an aperiodic set of prototiles; that is, a shape that can tessellate space but only in a nonperiodic way. Such a shape is called an einstein, a word play on ein Stein, German for "one stone". Several variants of the problem, depending on the particular definitions of nonperiodicity and the specifications of what sets may qualify as tiles and what types of matching rules are permitted, were solved beginning in the 1990s. The strictest version of the problem was solved in 2023, pending peer review. The einstein problem can be seen as a natural extension of the second part of Hilbert's eighteenth problem, which asks for a single polyhedron that tiles Euclidean 3-space, but such that no tessellation by this polyhedron is isohedral. Such anisohedral tiles were found by Karl Reinhardt in 1928, but these anisohedral tiles all tile space periodically.
In geometry, a plesiohedron is a special kind of space-filling polyhedron, defined as the Voronoi cell of a symmetric Delone set. Three-dimensional Euclidean space can be completely filled by copies of any one of these shapes, with no overlaps. The resulting honeycomb will have symmetries that take any copy of the plesiohedron to any other copy.

Chaim Goodman-Strauss is an American mathematician who works in convex geometry, especially aperiodic tiling. He is on the faculty of the University of Arkansas and currently serves as outreach mathematician for the National Museum of Mathematics. He is co-author with John H. Conway and Heidi Burgiel of The Symmetries of Things, a comprehensive book surveying the mathematical theory of patterns.

In geometry, a chair tiling is a nonperiodic substitution tiling created from L-tromino prototiles. These prototiles are examples of rep-tiles and so an iterative process of decomposing the L tiles into smaller copies and then rescaling them to their original size can be used to cover patches of the plane. Chair tilings do not possess translational symmetry, i.e., they are examples of nonperiodic tilings, but the chair tiles are not aperiodic tiles since they are not forced to tile nonperiodically by themselves. The trilobite and cross tiles are aperiodic tiles that enforce the chair tiling substitution structure and these tiles have been modified to a simple aperiodic set of tiles using matching rules enforcing the same structure. Barge et al. have computed the Čech cohomology of the chair tiling and it has been shown that chair tilings can also be obtained via a cut-and-project scheme.
Craig S. Kaplan is a Canadian computer scientist, mathematician, and mathematical artist. He is an editor of the Journal of Mathematics and the Arts, and an organizer of the Bridges Conference on mathematics and art. He is an associate professor of computer science at the University of Waterloo, Canada.

David Smith is a retired print technician from Bridlington, England who is best known for his discoveries related to aperiodic monotiles that helped to solve the einstein problem.