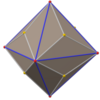
In geometry, a regular icosahedron is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.

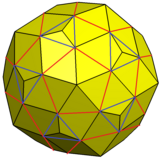
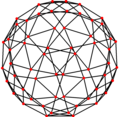
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.

In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. There are 13 Catalan solids. They are named for the Belgian mathematician Eugène Catalan, who first described them in 1865.

In geometry, a pentakis dodecahedron or kisdodecahedron is the polyhedron created by attaching a pentagonal pyramid to each face of a regular dodecahedron; that is, it is the Kleetope of the dodecahedron. It is a Catalan solid, meaning that it is a dual of an Archimedean solid, in this case, the truncated icosahedron.

In geometry, the deltoidal icositetrahedron is a Catalan solid. Its 24 faces are congruent kites. The deltoidal icositetrahedron, whose dual is the (uniform) rhombicuboctahedron, is tightly related to the pseudo-deltoidal icositetrahedron, whose dual is the pseudorhombicuboctahedron; but the actual and pseudo-d.i. are not to be confused with each other.

In geometry, a deltoidal hexecontahedron is a Catalan solid which is the dual polyhedron of the rhombicosidodecahedron, an Archimedean solid. It is one of six Catalan solids to not have a Hamiltonian path among its vertices.
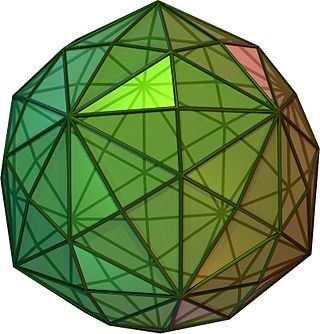
In geometry, a disdyakis triacontahedron, hexakis icosahedron, decakis dodecahedron or kisrhombic triacontahedron is a Catalan solid with 120 faces and the dual to the Archimedean truncated icosidodecahedron. As such it is face-uniform but with irregular face polygons. It slightly resembles an inflated rhombic triacontahedron: if one replaces each face of the rhombic triacontahedron with a single vertex and four triangles in a regular fashion, one ends up with a disdyakis triacontahedron. That is, the disdyakis triacontahedron is the Kleetope of the rhombic triacontahedron. It also has the most faces among the Archimedean and Catalan solids, with the snub dodecahedron, with 92 faces, in second place.

In geometry, the snub disphenoid, Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron is a convex polyhedron with twelve equilateral triangles as its faces. It is not a regular polyhedron because some vertices have four faces and others have five. It is a dodecahedron, one of the eight deltahedra, and is the 84th Johnson solid. It can be thought of as a square antiprism where both squares are replaced with two equilateral triangles.

In geometry, the small dodecicosidodecahedron (or small dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U33. It has 44 faces (20 triangles, 12 pentagons, and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the great snub icosidodecahedron is a nonconvex uniform polyhedron, indexed as U57. It has 92 faces (80 triangles and 12 pentagrams), 150 edges, and 60 vertices. It can be represented by a Schläfli symbol sr{5⁄2,3}, and Coxeter-Dynkin diagram .
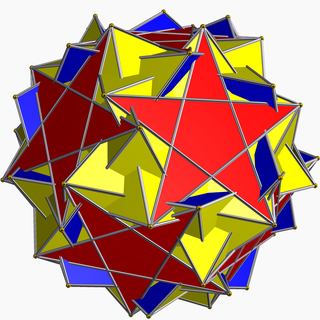
In geometry, the inverted snub dodecadodecahedron (or vertisnub dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U60. It is given a Schläfli symbol sr{5/3,5}.

In geometry, the great inverted snub icosidodecahedron (or great vertisnub icosidodecahedron) is a uniform star polyhedron, indexed as U69. It is given a Schläfli symbol sr{5⁄3,3}, and Coxeter-Dynkin diagram . In the book Polyhedron Models by Magnus Wenninger, the polyhedron is misnamed great snub icosidodecahedron, and vice versa.

A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals. It is represented by the Schläfli symbol {5,3}.

In geometry, the medial rhombic triacontahedron is a nonconvex isohedral polyhedron. It is a stellation of the rhombic triacontahedron, and can also be called small stellated triacontahedron. Its dual is the dodecadodecahedron.

In geometry, the great rhombic triacontahedron is a nonconvex isohedral, isotoxal polyhedron. It is the dual of the great icosidodecahedron (U54). Like the convex rhombic triacontahedron it has 30 rhombic faces, 60 edges and 32 vertices.

In geometry, the medial pentagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the snub dodecadodecahedron. It has 60 intersecting irregular pentagonal faces.

In geometry, the great pentagrammic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the great retrosnub icosidodecahedron. Its 60 faces are irregular pentagrams.

In geometry, the small hexagrammic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the small retrosnub icosicosidodecahedron. It is partially degenerate, having coincident vertices, as its dual has coplanar triangular faces.

In geometry, the small hexagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform small snub icosicosidodecahedron. It is partially degenerate, having coincident vertices, as its dual has coplanar triangular faces.

In geometry, the medial hexagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform snub icosidodecadodecahedron.