
In geometry, an Archimedean solid is one of 13 convex polyhedra whose faces are regular polygons and whose vertices are all symmetric to each other. They were first enumerated by Archimedes. They belong to the class of convex uniform polyhedra, the convex polyhedra with regular faces and symmetric vertices, which is divided into the Archimedean solids, the five Platonic solids, and the two infinite families of prisms and antiprisms. The pseudorhombicuboctahedron is an extra polyhedron with regular faces and congruent vertices, but it is not generally counted as an Archimedean solid because it is not vertex-transitive. An even larger class than the convex uniform polyhedra is the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices.

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.
In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, the regular icosahedron is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with regular faces to each of its pentagonal faces, or by putting points onto the cube. The resulting polyhedron has 20 equilateral triangles as its faces, 30 edges, and 12 vertices. It is an example of the Platonic solid and of the deltahedron. The icosahedral graph represents the skeleton of a regular icosahedron.
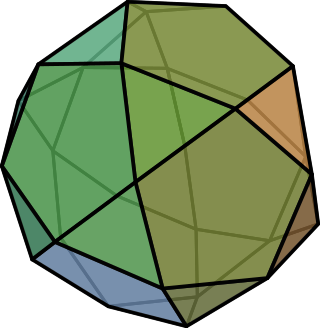
In geometry, an icosidodecahedron is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. There are only five such polyhedra:

In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square, it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in n dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word stellation comes from the Latin stellātus, "starred", which in turn comes from Latin stella, "star". Stellation is the reciprocal or dual process to faceting.

In geometry, the truncated cuboctahedron or great rhombicuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.
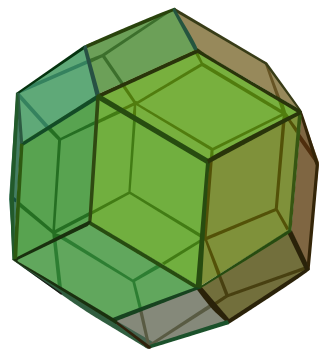
The rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Catalan solid, and the dual polyhedron of the icosidodecahedron. It is a zonohedron.

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids.

In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.
In geometry, a quasiregular polyhedron is a uniform polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are vertex-transitive and edge-transitive, hence a step closer to regular polyhedra than the semiregular, which are merely vertex-transitive.

In geometry, the Waterman polyhedra are a family of polyhedra discovered around 1990 by the mathematician Steve Waterman. A Waterman polyhedron is created by packing spheres according to the cubic close(st) packing (CCP), also known as the face-centered cubic (fcc) packing, then sweeping away the spheres that are farther from the center than a defined radius, then creating the convex hull of the sphere centers.

In geometry, a Schönhardt polyhedron is a polyhedron with the same combinatorial structure as a regular octahedron, but with dihedral angles that are non-convex along three disjoint edges. Because it has no interior diagonals, it cannot be triangulated into tetrahedra without adding new vertices. It has the fewest vertices of any polyhedron that cannot be triangulated. It is named after German mathematician Erich Schönhardt, who described it in 1928, although artist Karlis Johansons exhibited a related structure in 1921.

Jessen's icosahedron, sometimes called Jessen's orthogonal icosahedron, is a non-convex polyhedron with the same numbers of vertices, edges, and faces as the regular icosahedron. It is named for Børge Jessen, who studied it in 1967. In 1971, a family of nonconvex polyhedra including this shape was independently discovered and studied by Adrien Douady under the name six-beakedshaddock; later authors have applied variants of this name more specifically to Jessen's icosahedron.

In geometry, an icosahedron is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi) 'twenty', and ἕδρα (hédra) 'seat'. The plural can be either "icosahedra" or "icosahedrons".




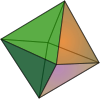












![Jessen's icosahedron. All dihedral angles are 90deg. The vertices of the inscribed cube are the centers of the equilateral triangle faces. The polyhedron is a construct of the lengths [?]1 [?]2 [?]3 [?]4 [?]5 [?]6 of Legendre's three-square theorem and the angles
/2
/3
/4. Jessen's icosahedron with dimensions.png](http://upload.wikimedia.org/wikipedia/commons/thumb/2/2c/Jessen%27s_icosahedron_with_dimensions.png/400px-Jessen%27s_icosahedron_with_dimensions.png)




















