In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).

In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra.

In mathematics, the Klein four-group is an abelian group with four elements, in which each element is self-inverse (composing it with itself produces the identity) and in which composing any two of the three non-identity elements produces the third one. It can be described as the symmetry group of a non-square rectangle (with the three non-identity elements being horizontal reflection, vertical reflection and 180-degree rotation), as the group of bitwise exclusive or operations on two-bit binary values, or more abstractly as Z2 × Z2, the direct product of two copies of the cyclic group of order 2. It was named Vierergruppe (German:[ˈfiːʁɐˌɡʁʊpə], meaning four-group) by Felix Klein in 1884. It is also called the Klein group, and is often symbolized by the letter V or as K4.

In mathematics, an alternating group is the group of even permutations of a finite set. The alternating group on a set of n elements is called the alternating group of degree n, or the alternating group on n letters and denoted by An or Alt(n).

In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.
In geometry, an improper rotation is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendicular to that axis. Reflection and inversion are each special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation. It is used as a symmetry operation in the context of geometric symmetry, molecular symmetry and crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have improper rotation symmetry.

In geometry, the truncated cuboctahedron or great rhombicuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

In mathematics, a Euclidean group is the group of (Euclidean) isometries of a Euclidean space ; that is, the transformations of that space that preserve the Euclidean distance between any two points (also called Euclidean transformations). The group depends only on the dimension n of the space, and is commonly denoted E(n) or ISO(n).
In crystallography, a crystallographic point group is a three dimensional point group whose symmetry operations are compatible with a three dimensional crystallographic lattice. According to the crystallographic restriction it may only contain one-, two-, three-, four- and sixfold rotations or rotoinversions. This reduces the number of crystallographic point groups to 32. These 32 groups are one-and-the-same as the 32 types of morphological (external) crystalline symmetries derived in 1830 by Johann Friedrich Christian Hessel from a consideration of observed crystal forms.

Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.
The Schoenfliesnotation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the symmetry of a molecule, the notation is often sufficient and commonly used for spectroscopy. However, in crystallography, there is additional translational symmetry, and point groups are not enough to describe the full symmetry of crystals, so the full space group is usually used instead. The naming of full space groups usually follows another common convention, the Hermann–Mauguin notation, also known as the international notation.
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.

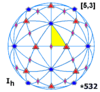
In mathematics, and especially in geometry, an object has icosahedral symmetry if it has the same symmetries as a regular icosahedron. Examples of other polyhedra with icosahedral symmetry include the regular dodecahedron and the rhombic triacontahedron.

A regular octahedron has 24 rotational symmetries, and 48 symmetries altogether. These include transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the polyhedron that is dual to an octahedron.
In a group, the conjugate by g of h is ghg−1.

In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries (isometries) that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O(2), including O(2) itself. Its elements are rotations and reflections, and every such group containing only rotations is a subgroup of the special orthogonal group SO(2), including SO(2) itself. That group is isomorphic to R/Z and the first unitary group, U(1), a group also known as the circle group.
In mathematics, the generalized dihedral groups are a family of groups with algebraic structures similar to that of the dihedral groups. They include the finite dihedral groups, the infinite dihedral group, and the orthogonal group O(2). Dihedral groups play an important role in group theory, geometry, and chemistry.
In geometry, the polyhedral group is any of the symmetry groups of the Platonic solids.

In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson.
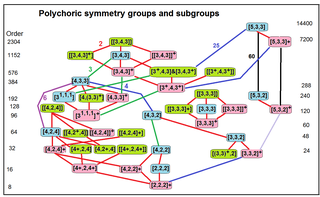
In geometry, a point group in four dimensions is an isometry group in four dimensions that leaves the origin fixed, or correspondingly, an isometry group of a 3-sphere.