In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies of an n-sided polygon, connected by an alternating band of 2n triangles. They are represented by the Conway notation An.

In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides ; it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform before they refer to it as a “Johnson solid”.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

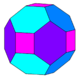
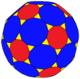
In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

In geometry, a deltahedron is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek upper case delta (Δ), which has the shape of an equilateral triangle. There are infinitely many deltahedra, all having an even number of faces by the handshaking lemma. Of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces. The number of faces, edges, and vertices is listed below for each of the eight convex deltahedra.
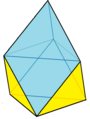
In geometry, the triangular bipyramid is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.

In geometry, the triaugmented triangular prism is a convex polyhedron with 14 equilateral triangles as its faces. Also called the tetracaidecadeltahedron, tetrakaidecadeltahedron, tetrakis triangular prism, or tricapped trigonal prism, it is an example of a deltahedron and a Johnson solid. It can be constructed by attaching equilateral square pyramids to each of the three square faces of a triangular prism.

In geometry, the gyrobifastigium is the 26th Johnson solid. It can be constructed by joining two face-regular triangular prisms along corresponding square faces, giving a quarter-turn to one prism. It is the only Johnson solid that can tile three-dimensional space.
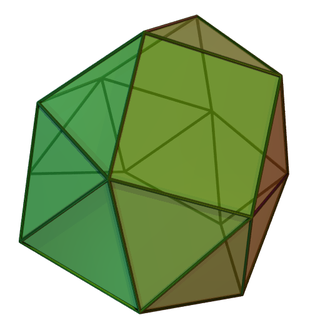
In geometry, the gyroelongated triangular cupola is one of the Johnson solids (J22). It can be constructed by attaching a hexagonal antiprism to the base of a triangular cupola (J3). This is called "gyroelongation", which means that an antiprism is joined to the base of a solid, or between the bases of more than one solid.

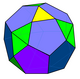
In geometry, the augmented truncated tetrahedron is one of the Johnson solids. It is created by attaching a triangular cupola to one hexagonal face of a truncated tetrahedron.

In geometry, the square antiprism is the second in an infinite family of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It is also known as an anticube.

In geometry, the truncated triakis tetrahedron, or more precisely an order-6 truncated triakis tetrahedron, is a convex polyhedron with 16 faces: 4 sets of 3 pentagons arranged in a tetrahedral arrangement, with 4 hexagons in the gaps.
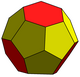
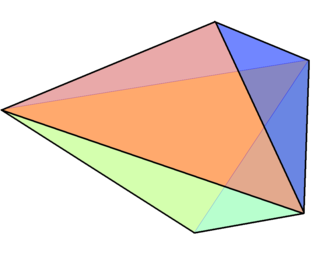
A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.

In geometry, the gyroelongated cupolae are an infinite set of polyhedra, constructed by adjoining an n-gonal cupola to an 2n-gonal antiprism.

In geometry, the gyroelongated bicupolae are an infinite sets of polyhedra, constructed by adjoining two n-gonal cupolas to an n-gonal Antiprism. The triangular, square, and pentagonal gyroelongated bicupola are three of five Johnson solids which are chiral, meaning that they have a "left-handed" and a "right-handed" form.
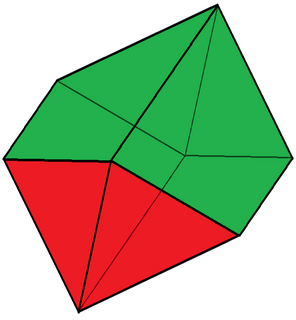
In geometry, an elongated octahedron is a polyhedron with 8 faces, 14 edges, and 8 vertices.

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.

In geometry, an icosahedron is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi) 'twenty' and from Ancient Greek ἕδρα (hédra) ' seat'. The plural can be either "icosahedra" or "icosahedrons".