In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two pyramids together base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base vertices are usually coplanar and a bipyramid is usually symmetric, meaning the two pyramids are mirror images across their common base plane. When each apex of the bipyramid is on a line perpendicular to the base and passing through its center, it is a right bipyramid; otherwise it is oblique. When the base is a regular polygon, the bipyramid is also called regular.

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.

In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

In geometry, a regular icosahedron is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.
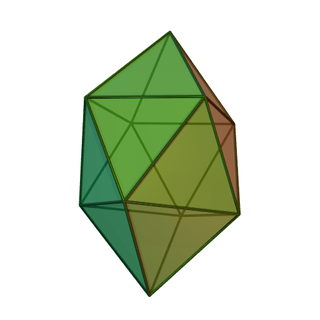
In geometry, the gyroelongated square bipyramid, heccaidecadeltahedron, or tetrakis square antiprism is a polyhedron with 16 triangular faces, constructed by attaching two equilateral square pyramids onto the face of a square antiprism. All of its triangular faces are equilateral, making it one of the eight convex deltahedra.

The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron and of a Johnson solid.

In geometry, a square pyramid is a pyramid with a square base, having a total of five faces. If the apex of the pyramid is directly above the center of the square, it is a right square pyramid with four isosceles triangles; otherwise, it is an oblique square pyramid. When all of the pyramid's edges are equal in length, its triangles are all equilateral, and it is called an equilateral square pyramid.

In geometry, the snub disphenoid, Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron is a convex polyhedron with twelve equilateral triangles as its faces. It is not a regular polyhedron because some vertices have four faces and others have five. It is a dodecahedron, one of the eight convex deltahedra, and is the 84th Johnson solid. It can be thought of as a square antiprism where both squares are replaced with two equilateral triangles.

In geometry, the elongated square bipyramid is the polyhedron constructed by attaching two equilateral square pyramids onto a cube's faces that are opposite each other. It can also be seen as 4 lunes linked together with squares to squares and triangles to triangles. It is also been named the pencil cube or 12-faced pencil cube due to its shape.
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. It is a conic solid with a polygonal base. Many types of pyramids can be found by determining the shape of bases, or cutting off the apex. It can be generalized into higher dimension, known as hyperpyramid. All pyramids are self-dual.

In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals all have midspheres. The radius of the midsphere is called the midradius. A polyhedron that has a midsphere is said to be midscribed about this sphere.
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.

In geometry, the Schönhardt polyhedron is the simplest non-convex polyhedron that cannot be triangulated into tetrahedra without adding new vertices. It is named after German mathematician Erich Schönhardt, who described it in 1928. The same polyhedra have also been studied in connection with Cauchy's rigidity theorem as an example where polyhedra with two different shapes have faces of the same shapes.
In geometry and polyhedral combinatorics, the Kleetope of a polyhedron or higher-dimensional convex polytope P is another polyhedron or polytope PK formed by replacing each facet of P with a shallow pyramid. Kleetopes are named after Victor Klee.
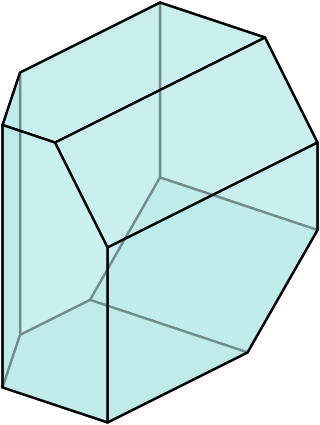
In geometry, an enneahedron is a polyhedron with nine faces. There are 2606 types of convex enneahedron, each having a different pattern of vertex, edge, and face connections. None of them are regular.

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.

In three-dimensional hyperbolic geometry, an ideal polyhedron is a convex polyhedron all of whose vertices are ideal points, points "at infinity" rather than interior to three-dimensional hyperbolic space. It can be defined as the convex hull of a finite set of ideal points. An ideal polyhedron has ideal polygons as its faces, meeting along lines of the hyperbolic space.
































