Related Research Articles

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.

In mathematics, especially order theory, a partial order on a set is an arrangement such that, for certain pairs of elements, one precedes the other. The word partial is used to indicate that not every pair of elements needs to be comparable; that is, there may be pairs for which neither element precedes the other. Partial orders thus generalize total orders, in which every pair is comparable.

In mathematics, the power set (or powerset) of a set S is the set of all subsets of S, including the empty set and S itself. In axiomatic set theory (as developed, for example, in the ZFC axioms), the existence of the power set of any set is postulated by the axiom of power set. The powerset of S is variously denoted as P(S), 𝒫(S), P(S), , , or 2S. The notation 2S, meaning the set of all functions from S to a given set of two elements (e.g., {0, 1}), is used because the powerset of S can be identified with, is equivalent to, or bijective to the set of all the functions from S to the given two-element set.
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum (join) and an infimum (meet). A lattice which satisfies at least one of these properties is known as a conditionally complete lattice. For comparison, in a general lattice, only pairs of elements need to have a supremum and an infimum. Every non-empty finite lattice is complete, but infinite lattices may be incomplete.

In mathematics, a category is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions.
In category theory, an epimorphism is a morphism f : X → Y that is right-cancellative in the sense that, for all objects Z and all morphisms g1, g2: Y → Z,
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.
In mathematics, a distributive lattice is a lattice in which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to isomorphism—given as such a lattice of sets.
In mathematics, the Boolean prime ideal theorem states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on sets is known as the ultrafilter lemma. Other theorems are obtained by considering different mathematical structures with appropriate notions of ideals, for example, rings and prime ideals, or distributive lattices and maximal ideals. This article focuses on prime ideal theorems from order theory.
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary.
This is a glossary of some terms used in various branches of mathematics that are related to the fields of order, lattice, and domain theory. Note that there is a structured list of order topics available as well. Other helpful resources might be the following overview articles:

In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included. Antimatroids are commonly axiomatized in two equivalent ways, either as a set system modeling the possible states of such a process, or as a formal language modeling the different sequences in which elements may be included. Dilworth (1940) was the first to study antimatroids, using yet another axiomatization based on lattice theory, and they have been frequently rediscovered in other contexts.
In mathematical logic, a Boolean-valued model is a generalization of the ordinary Tarskian notion of structure from model theory. In a Boolean-valued model, the truth values of propositions are not limited to "true" and "false", but instead take values in some fixed complete Boolean algebra.
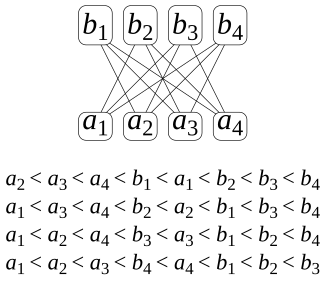
In mathematics, the dimension of a partially ordered set (poset) is the smallest number of total orders the intersection of which gives rise to the partial order. This concept is also sometimes called the order dimension or the Dushnik–Miller dimension of the partial order. Dushnik & Miller (1941) first studied order dimension; for a more detailed treatment of this subject than provided here, see Trotter (1992).
Boolean algebra is a mathematically rich branch of abstract algebra. Stanford Encyclopaedia of Philosophy defines Boolean algebra as 'the algebra of two-valued logic with only sentential connectives, or equivalently of algebras of sets under union and complementation.' Just as group theory deals with groups, and linear algebra with vector spaces, Boolean algebras are models of the equational theory of the two values 0 and 1. Common to Boolean algebras, groups, and vector spaces is the notion of an algebraic structure, a set closed under some operations satisfying certain equations.
In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order. Comparability graphs have also been called transitively orientable graphs, partially orderable graphs, containment graphs, and divisor graphs. An incomparability graph is an undirected graph that connects pairs of elements that are not comparable to each other in a partial order.
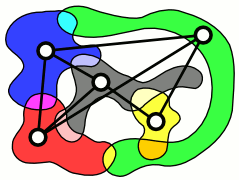
In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types of sets that are used to form an intersection representation of them.
In the mathematical field of order theory, an inclusion order is the partial order that arises as the subset-inclusion relation on some collection of objects. In a simple way, every poset P = (X,≤) is (isomorphic to) an inclusion order (just as every group is isomorphic to a permutation group – see Cayley's theorem). To see this, associate to each element x of X the set
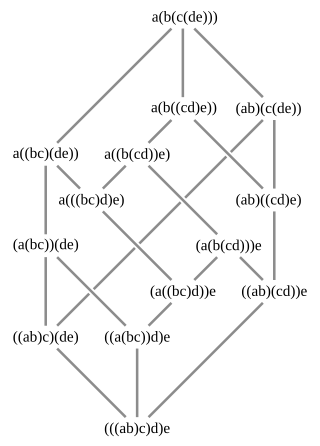
In mathematics, a Tamari lattice, introduced by Dov Tamari (1962), is a partially ordered set in which the elements consist of different ways of grouping a sequence of objects into pairs using parentheses; for instance, for a sequence of four objects abcd, the five possible groupings are ((ab)c)d, (ab)(cd), (a(bc))d, a((bc)d), and a(b(cd)). Each grouping describes a different order in which the objects may be combined by a binary operation; in the Tamari lattice, one grouping is ordered before another if the second grouping may be obtained from the first by only rightward applications of the associative law (xy)z = x(yz). For instance, applying this law with x = a, y = bc, and z = d gives the expansion (a(bc))d = a((bc)d), so in the ordering of the Tamari lattice (a(bc))d ≤ a((bc)d).
In mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets. The theorem can be interpreted as providing a one-to-one correspondence between distributive lattices and partial orders, between quasi-ordinal knowledge spaces and preorders, or between finite topological spaces and preorders. It is named after Garrett Birkhoff, who published a proof of it in 1937.
References
- ↑ Weisstein, Eric W. "Group Representation". mathworld.wolfram.com. Retrieved 2019-12-07.
- 1 2 Teleman, Constantin. "Representation Theory" (PDF). math.berkeley.edu. Retrieved 2019-12-07.
- ↑ McKee, Terry A.; McMorris, F. R. (1999), Topics in Intersection Graph Theory, SIAM Monographs on Discrete Mathematics and Applications, Philadelphia: Society for Industrial and Applied Mathematics, doi:10.1137/1.9780898719802, ISBN 978-0-89871-430-2, MR 1672910
- ↑ Erdős, Paul; Goodman, A. W.; Pósa, Louis (1966), "The representation of a graph by set intersections", Canadian Journal of Mathematics , 18 (1): 106–112, CiteSeerX 10.1.1.210.6950 , doi:10.4153/cjm-1966-014-3, MR 0186575
- ↑ Biggs, Norman (1994), Algebraic Graph Theory, Cambridge Mathematical Library, Cambridge University Press, ISBN 978-0-521-45897-9, MR 1271140
- ↑ Trotter, William T. (1992), Combinatorics and Partially Ordered Sets: Dimension Theory, Johns Hopkins Series in the Mathematical Sciences, Baltimore: The Johns Hopkins University Press, ISBN 978-0-8018-4425-6, MR 1169299
- ↑ Scheinerman, Edward (1991), "A note on planar graphs and circle orders", SIAM Journal on Discrete Mathematics , 4 (3): 448–451, doi:10.1137/0404040, MR 1105950
- ↑ Fishburn, Peter C. (1985), Interval Orders and Interval Graphs: A Study of Partially Ordered Sets, Wiley-Interscience Series in Discrete Mathematics, John Wiley & Sons, ISBN 978-0-471-81284-5, MR 0776781
- ↑ Marshall H. Stone (1936) "The Theory of Representations of Boolean Algebras," Transactions of the American Mathematical Society 40: 37-111.
- ↑ Esakia, Leo (1974). "Topological Kripke models". Soviet Math. 15 (1): 147–151.
- ↑ Hirsch, R.; Hodkinson, I. (2002). Relation Algebra by Games. Studies in Logic and the Foundations of Mathematics. Vol. 147. Elsevier Science.
- ↑ Tanenbaum, Paul J. (1999), "Simultaneous intersection representation of pairs of graphs", Journal of Graph Theory , 32 (2): 171–190, doi:10.1002/(SICI)1097-0118(199910)32:2<171::AID-JGT7>3.0.CO;2-N, MR 1709659
- ↑ Fischermann, Miranca; Knoben, Werner; Kremer, Dirk; Rautenbachh, Dieter (2004), "Competition polysemy", Discrete Mathematics , 282 (1–3): 251–255, doi: 10.1016/j.disc.2003.11.014 , MR 2059526
- ↑ Tanenbaum, Paul J. (1996), "Simultaneous representation of interval and interval-containment orders", Order , 13 (4): 339–350, CiteSeerX 10.1.1.53.8988 , doi:10.1007/BF00405593, MR 1452517, S2CID 16904281