The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other; thus, a solution requires that no two queens share the same row, column, or diagonal. There are 92 solutions. The problem was first posed in the mid-19th century. In the modern era, it is often used as an example problem for various computer programming techniques.

The Sierpiński triangle, also called the Sierpiński gasket or Sierpiński sieve, is a fractal attractive fixed set with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. Originally constructed as a curve, this is one of the basic examples of self-similar sets—that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries before the work of Sierpiński.

The Tower of Hanoi is a mathematical game or puzzle consisting of three rods and a number of disks of various diameters, which can slide onto any rod. The puzzle begins with the disks stacked on one rod in order of decreasing size, the smallest at the top, thus approximating a conical shape. The objective of the puzzle is to move the entire stack to one of the other rods, obeying the following rules:
- Only one disk may be moved at a time.
- Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
- No disk may be placed on top of a disk that is smaller than it.
Graham's number is a large number that arose as an upper bound on the answer of a problem in the mathematical field of Ramsey theory. It is much larger than many other large numbers such as Skewes's number and Moser's number, both of which are in turn much larger than a googolplex. As with these, it is so large that the observable universe is far too small to contain an ordinary digital representation of Graham's number, assuming that each digit occupies one Planck volume, possibly the smallest measurable space. But even the number of digits in this digital representation of Graham's number would itself be a number so large that its digital representation cannot be represented in the observable universe. Nor even can the number of digits of that number—and so forth, for a number of times far exceeding the total number of Planck volumes in the observable universe. Thus Graham's number cannot be expressed even by physical universe-scale power towers of the form .
The On-Line Encyclopedia of Integer Sequences (OEIS) is an online database of integer sequences. It was created and maintained by Neil Sloane while researching at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to the OEIS Foundation in 2009. Sloane is the chairman of the OEIS Foundation.
The Wedderburn–Etherington numbers are an integer sequence named for Ivor Malcolm Haddon Etherington and Joseph Wedderburn that can be used to count certain kinds of binary trees. The first few numbers in the sequence are
171 is the natural number following 170 and preceding 172.
God's algorithm is a notion originating in discussions of ways to solve the Rubik's Cube puzzle, but which can also be applied to other combinatorial puzzles and mathematical games. It refers to any algorithm which produces a solution having the fewest possible moves. The allusion to the deity is based on the notion that an omniscient being would know an optimal step from any given configuration.
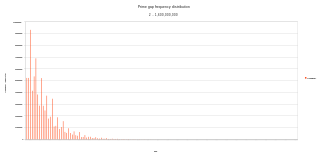
A prime gap is the difference between two successive prime numbers. The n-th prime gap, denoted gn or g(pn) is the difference between the (n + 1)-st and the n-th prime numbers, i.e.
5 (five) is a number, numeral and digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number. It has garnered attention throughout history in part because distal extremities in humans typically contain five digits.

In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the number of weak orderings on a set of elements. Weak orderings arrange their elements into a sequence allowing ties, such as might arise as the outcome of a horse race). Starting from , these numbers are

A double exponential function is a constant raised to the power of an exponential function. The general formula is (where a>1 and b>1), which grows much more quickly than an exponential function. For example, if a = b = 10:

In geometry, a domino tiling of a region in the Euclidean plane is a tessellation of the region by dominoes, shapes formed by the union of two unit squares meeting edge-to-edge. Equivalently, it is a perfect matching in the grid graph formed by placing a vertex at the center of each square of the region and connecting two vertices when they correspond to adjacent squares.
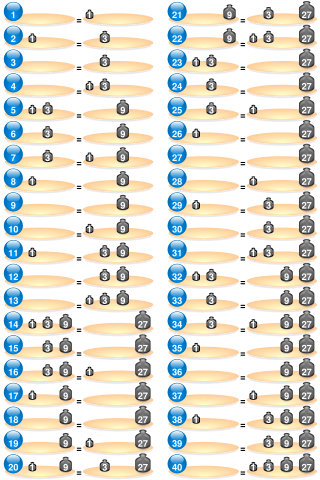
In mathematics, a power of three is a number of the form 3n where n is an integer, that is, the result of exponentiation with number three as the base and integer n as the exponent.

In mathematics, the telephone numbers or the involution numbers form a sequence of integers that count the ways n people can be connected by person-to-person telephone calls. These numbers also describe the number of matchings of a complete graph on n vertices, the number of permutations on n elements that are involutions, the sum of absolute values of coefficients of the Hermite polynomials, the number of standard Young tableaux with n cells, and the sum of the degrees of the irreducible representations of the symmetric group. Involution numbers were first studied in 1800 by Heinrich August Rothe, who gave a recurrence equation by which they may be calculated, giving the values

In number theory, Firoozbakht's conjecture is a conjecture about the distribution of prime numbers. It is named after the Iranian mathematician Farideh Firoozbakht who stated it first in 1982.

The Magnetic Tower of Hanoi (MToH) puzzle is a variation of the classical Tower of Hanoi puzzle (ToH), where each disk has two distinct sides, for example, with different colors "red" and "blue". The rules of the MToH puzzle are the same as the rules of the original puzzle, with the added constraints that each disk is flipped as it is moved, and that two disks may not be placed one on another if their touching sides have the same color. Each disk has a North and South pole, with similar poles repelling one another and opposite poles attracting one another. Magnets inside each disk physically prevent illegal moves.
In combinatorial mathematics and statistics, the Fuss–Catalan numbers are numbers of the form

In graph theory and recreational mathematics, the Hanoi graphs are undirected graphs whose vertices represent the possible states of the Tower of Hanoi puzzle, and whose edges represent allowable moves between pairs of states.
In mathematics, a Stanley sequence is an integer sequence generated by a greedy algorithm that chooses the sequence members to avoid arithmetic progressions. If is a finite set of non-negative integers on which no three elements form an arithmetic progression, then the Stanley sequence generated from starts from the elements of , in sorted order, and then repeatedly chooses each successive element of the sequence to be a number that is larger than the already-chosen numbers and does not form any three-term arithmetic progression with them. These sequences are named after Richard P. Stanley.












