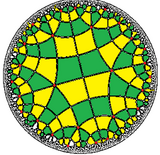
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises by either replacing the parallel postulate with an alternative, or relaxing the metric requirement. In the former case, one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras, which give rise to kinematic geometries that have also been called non-Euclidean geometry.

In geometry, a trapezoid in North American English, or trapezium in British English, is a quadrilateral that has at least one pair of parallel sides.

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

In Euclidean geometry, an isosceles trapezoid is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined as a trapezoid in which both legs and both base angles are of equal measure, or as a trapezoid whose diagonals have equal length. Note that a non-rectangular parallelogram is not an isosceles trapezoid because of the second condition, or because it has no line of symmetry. In any isosceles trapezoid, two opposite sides are parallel, and the two other sides are of equal length, and the diagonals have equal length. The base angles of an isosceles trapezoid are equal in measure.
Absolute geometry is a geometry based on an axiom system for Euclidean geometry without the parallel postulate or any of its alternatives. Traditionally, this has meant using only the first four of Euclid's postulates. The term was introduced by János Bolyai in 1832. It is sometimes referred to as neutral geometry, as it is neutral with respect to the parallel postulate. The first four of Euclid's postulates are now considered insufficient as a basis of Euclidean geometry, so other systems are used instead.

In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of xy = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation.

In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.
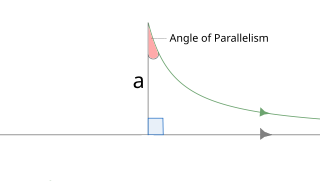
In hyperbolic geometry, angle of parallelism is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.
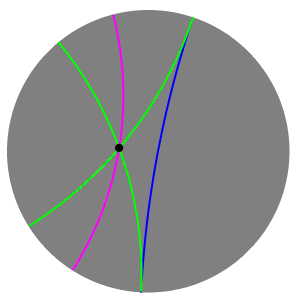
In hyperbolic geometry, two lines are said to be ultraparallel if they do not intersect and are not limiting parallel.
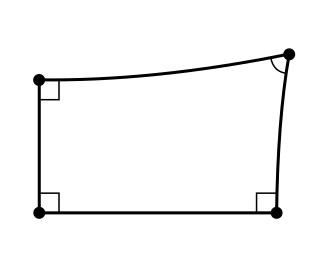
In geometry, a Lambert quadrilateral, is a quadrilateral in which three of its angles are right angles. Historically, the fourth angle of a Lambert quadrilateral was of considerable interest since if it could be shown to be a right angle, then the Euclidean parallel postulate could be proved as a theorem. It is now known that the type of the fourth angle depends upon the geometry in which the quadrilateral exists. In hyperbolic geometry the fourth angle is acute, in Euclidean geometry it is a right angle and in elliptic geometry it is an obtuse angle.
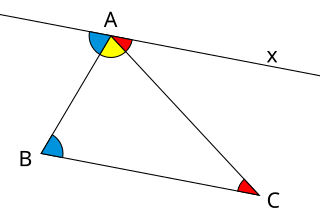
In a Euclidean space, the sum of angles of a triangle equals the straight angle . A triangle has three angles, one at each vertex, bounded by a pair of adjacent sides.

In hyperbolic geometry, a hypercycle, hypercircle or equidistant curve is a curve whose points have the same orthogonal distance from a given straight line.

Giordano Vitale or Vitale Giordano was an Italian mathematician. He is best known for his theorem on Saccheri quadrilaterals. He may also be referred to as Vitale Giordani, Vitale Giordano da Bitonto, and simply Giordano.
The exterior angle theorem is Proposition 1.16 in Euclid's Elements, which states that the measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. This is a fundamental result in absolute geometry because its proof does not depend upon the parallel postulate.

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides and opposite respective angles and , the law of cosines states:
Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.

Giovanni Girolamo Saccheri was an Italian Jesuit priest, scholastic philosopher, and mathematician. He is considered the forerunner of non-Euclidean geometry.
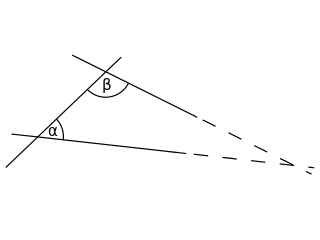
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
If a line segment intersects two straight lines forming two interior angles on the same side that are less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.
In the hyperbolic plane, as in the Euclidean plane, each point can be uniquely identified by two real numbers. Several qualitatively different ways of coordinatizing the plane in hyperbolic geometry are used.