In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy. Its spectrum, the system's energy spectrum or its set of energy eigenvalues, is the set of possible outcomes obtainable from a measurement of the system's total energy. Due to its close relation to the energy spectrum and time-evolution of a system, it is of fundamental importance in most formulations of quantum theory.
In quantum mechanics, identical particles are particles that cannot be distinguished from one another, even in principle. Species of identical particles include, but are not limited to, elementary particles, composite subatomic particles, as well as atoms and molecules. Quasiparticles also behave in this way. Although all known indistinguishable particles only exist at the quantum scale, there is no exhaustive list of all possible sorts of particles nor a clear-cut limit of applicability, as explored in quantum statistics. They were first discussed by Werner Heisenberg and Paul Dirac in 1926.
Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor. It is one of the few known quantum algorithms with compelling potential applications and strong evidence of superpolynomial speedup compared to best known classical algorithms. On the other hand, factoring numbers of practical significance requires far more qubits than available in the near future. Another concern is that noise in quantum circuits may undermine results, requiring additional qubits for quantum error correction.
In quantum computing, Grover's algorithm, also known as the quantum search algorithm, is a quantum algorithm for unstructured search that finds with high probability the unique input to a black box function that produces a particular output value, using just evaluations of the function, where is the size of the function's domain. It was devised by Lov Grover in 1996.
The Fock space is an algebraic construction used in quantum mechanics to construct the quantum states space of a variable or unknown number of identical particles from a single particle Hilbert space H. It is named after V. A. Fock who first introduced it in his 1932 paper "Konfigurationsraum und zweite Quantelung".
In physics, an operator is a function over a space of physical states onto another space of physical states. The simplest example of the utility of operators is the study of symmetry. Because of this, they are useful tools in classical mechanics. Operators are even more important in quantum mechanics, where they form an intrinsic part of the formulation of the theory.
The Deutsch–Jozsa algorithm is a deterministic quantum algorithm proposed by David Deutsch and Richard Jozsa in 1992 with improvements by Richard Cleve, Artur Ekert, Chiara Macchiavello, and Michele Mosca in 1998. Although of little practical use, it is one of the first examples of a quantum algorithm that is exponentially faster than any possible deterministic classical algorithm.
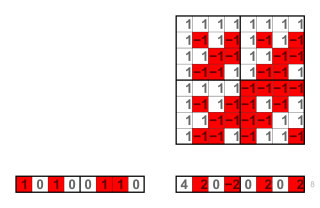
The Hadamard transform is an example of a generalized class of Fourier transforms. It performs an orthogonal, symmetric, involutive, linear operation on 2m real numbers.
In quantum computing and specifically the quantum circuit model of computation, a quantum logic gate is a basic quantum circuit operating on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.

In computer science, the controlled NOT gate, controlled-X gate, controlled-bit-flip gate, Feynman gate or controlled Pauli-X is a quantum logic gate that is an essential component in the construction of a gate-based quantum computer. It can be used to entangle and disentangle Bell states. Any quantum circuit can be simulated to an arbitrary degree of accuracy using a combination of CNOT gates and single qubit rotations. The gate is sometimes named after Richard Feynman who developed an early notation for quantum gate diagrams in 1986.
The hidden subgroup problem (HSP) is a topic of research in mathematics and theoretical computer science. The framework captures problems such as factoring, discrete logarithm, graph isomorphism, and the shortest vector problem. This makes it especially important in the theory of quantum computing because Shor's algorithm for factoring in quantum computing is an instance of the hidden subgroup problem for finite abelian groups, while the other problems correspond to finite groups that are not abelian.
Quantum walks are quantum analogues of classical random walks. In contrast to the classical random walk, where the walker occupies definite states and the randomness arises due to stochastic transitions between states, in quantum walks randomness arises through: (1) quantum superposition of states, (2) non-random, reversible unitary evolution and (3) collapse of the wave function due to state measurements.
The partition function or configuration integral, as used in probability theory, information theory and dynamical systems, is a generalization of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann distribution. The partition function occurs in many problems of probability theory because, in situations where there is a natural symmetry, its associated probability measure, the Gibbs measure, has the Markov property. This means that the partition function occurs not only in physical systems with translation symmetry, but also in such varied settings as neural networks, and applications such as genomics, corpus linguistics and artificial intelligence, which employ Markov networks, and Markov logic networks. The Gibbs measure is also the unique measure that has the property of maximizing the entropy for a fixed expectation value of the energy; this underlies the appearance of the partition function in maximum entropy methods and the algorithms derived therefrom.
In quantum information theory, a set of bases in Hilbert space Cd are are said to be mutually unbiased to mean, that, if a system is prepared in an eigen state of one of the bases, then all outcomes of the measurement with respect to the other basis are predicted to occur with an equal probability inexorably equal to 1/d.
A locally decodable code (LDC) is an error-correcting code that allows a single bit of the original message to be decoded with high probability by only examining a small number of bits of a possibly corrupted codeword. This property could be useful, say, in a context where information is being transmitted over a noisy channel, and only a small subset of the data is required at a particular time and there is no need to decode the entire message at once. Note that locally decodable codes are not a subset of locally testable codes, though there is some overlap between the two.
In quantum computing, the quantum phase estimation algorithm is a quantum algorithm to estimate the phase corresponding to an eigenvalue of a given unitary operator. Because the eigenvalues of a unitary operator always have unit modulus, they are characterized by their phase, and therefore the algorithm can be equivalently described as retrieving either the phase or the eigenvalue itself. The algorithm was initially introduced by Alexei Kitaev in 1995.
In quantum computing, the quantum Fourier transform (QFT) is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform. The quantum Fourier transform is a part of many quantum algorithms, notably Shor's algorithm for factoring and computing the discrete logarithm, the quantum phase estimation algorithm for estimating the eigenvalues of a unitary operator, and algorithms for the hidden subgroup problem. The quantum Fourier transform was discovered by Don Coppersmith.
Quantum optimization algorithms are quantum algorithms that are used to solve optimization problems. Mathematical optimization deals with finding the best solution to a problem from a set of possible solutions. Mostly, the optimization problem is formulated as a minimization problem, where one tries to minimize an error which depends on the solution: the optimal solution has the minimal error. Different optimization techniques are applied in various fields such as mechanics, economics and engineering, and as the complexity and amount of data involved rise, more efficient ways of solving optimization problems are needed. Quantum computing may allow problems which are not practically feasible on classical computers to be solved, or suggest a considerable speed up with respect to the best known classical algorithm.
Quantum counting algorithm is a quantum algorithm for efficiently counting the number of solutions for a given search problem. The algorithm is based on the quantum phase estimation algorithm and on Grover's search algorithm.

The Bernstein–Vazirani algorithm, which solves the Bernstein–Vazirani problem, is a quantum algorithm invented by Ethan Bernstein and Umesh Vazirani in 1997. It is a restricted version of the Deutsch–Jozsa algorithm where instead of distinguishing between two different classes of functions, it tries to learn a string encoded in a function. The Bernstein–Vazirani algorithm was designed to prove an oracle separation between complexity classes BQP and BPP.






































































































