The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. This mathematical formalism uses mainly a part of functional analysis, especially Hilbert spaces, which are a kind of linear space. Such are distinguished from mathematical formalisms for physics theories developed prior to the early 1900s by the use of abstract mathematical structures, such as infinite-dimensional Hilbert spaces, and operators on these spaces. In brief, values of physical observables such as energy and momentum were no longer considered as values of functions on phase space, but as eigenvalues; more precisely as spectral values of linear operators in Hilbert space.
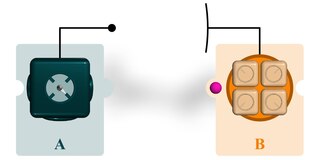
Quantum teleportation is a technique for transferring quantum information from a sender at one location to a receiver some distance away. While teleportation is commonly portrayed in science fiction as a means to transfer physical objects from one location to the next, quantum teleportation only transfers quantum information. The sender does not have to know the particular quantum state being transferred. Moreover, the location of the recipient can be unknown, but to complete the quantum teleportation, classical information needs to be sent from sender to receiver. Because classical information needs to be sent, quantum teleportation cannot occur faster than the speed of light.
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way.
In physics, the CHSH inequality can be used in the proof of Bell's theorem, which states that certain consequences of entanglement in quantum mechanics cannot be reproduced by local hidden-variable theories. Experimental verification of the inequality being violated is seen as confirmation that nature cannot be described by such theories. CHSH stands for John Clauser, Michael Horne, Abner Shimony, and Richard Holt, who described it in a much-cited paper published in 1969. They derived the CHSH inequality, which, as with John Stewart Bell's original inequality, is a constraint on the statistical occurrence of "coincidences" in a Bell test which is necessarily true if there exist underlying local hidden variables, an assumption that is sometimes termed local realism. In practice, the inequality is routinely violated by modern experiments in quantum mechanics.

Quantum decoherence is the loss of quantum coherence, the process in which a system's behaviour changes from that which can be explained by quantum mechanics to that which can be explained by classical mechanics. In quantum mechanics, particles such as electrons are described by a wave function, a mathematical representation of the quantum state of a system; a probabilistic interpretation of the wave function is used to explain various quantum effects. As long as there exists a definite phase relation between different states, the system is said to be coherent. A definite phase relationship is necessary to perform quantum computing on quantum information encoded in quantum states. Coherence is preserved under the laws of quantum physics.
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function. The partial trace has applications in quantum information and decoherence which is relevant for quantum measurement and thereby to the decoherent approaches to interpretations of quantum mechanics, including consistent histories and the relative state interpretation.
In mathematics, particularly in functional analysis, a projection-valued measure (PVM) is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a fixed Hilbert space. Projection-valued measures are formally similar to real-valued measures, except that their values are self-adjoint projections rather than real numbers. As in the case of ordinary measures, it is possible to integrate complex-valued functions with respect to a PVM; the result of such an integration is a linear operator on the given Hilbert space.

LOCC, or local operations and classical communication, is a method in quantum information theory where a local (product) operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed conditioned on the information received.
In functional analysis and quantum information science, a positive operator-valued measure (POVM) is a measure whose values are positive semi-definite operators on a Hilbert space. POVMs are a generalization of projection-valued measures (PVM) and, correspondingly, quantum measurements described by POVMs are a generalization of quantum measurement described by PVMs.
In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors
CEILIDH is a public key cryptosystem based on the discrete logarithm problem in algebraic torus. This idea was first introduced by Alice Silverberg and Karl Rubin in 2003; Silverberg named CEILIDH after her cat. The main advantage of the system is the reduced size of the keys for the same security over basic schemes.
A decoherence-free subspace (DFS) is a subspace of a quantum system's Hilbert space that is invariant to non-unitary dynamics. Alternatively stated, they are a small section of the system Hilbert space where the system is decoupled from the environment and thus its evolution is completely unitary. DFSs can also be characterized as a special class of quantum error correcting codes. In this representation they are passive error-preventing codes since these subspaces are encoded with information that (possibly) won't require any active stabilization methods. These subspaces prevent destructive environmental interactions by isolating quantum information. As such, they are an important subject in quantum computing, where (coherent) control of quantum systems is the desired goal. Decoherence creates problems in this regard by causing loss of coherence between the quantum states of a system and therefore the decay of their interference terms, thus leading to loss of information from the (open) quantum system to the surrounding environment. Since quantum computers cannot be isolated from their environment and information can be lost, the study of DFSs is important for the implementation of quantum computers into the real world.

In the context of quantum mechanics and quantum information theory, symmetric, informationally complete, positive operator-valued measures (SIC-POVMs) are a particular type of generalized measurement (POVM). SIC-POVMs are particularly notable thanks to their defining features of (1) being informationally complete; (2)having the minimal number of outcomes compatible with informational completeness, and (3) being highly symmetric. In this context, informational completeness is the property of a POVM of allowing to fully reconstruct input states from measurement data.
Entanglement distillation is the transformation of N copies of an arbitrary entangled state into some number of approximately pure Bell pairs, using only local operations and classical communication.
A quantum depolarizing channel is a model for quantum noise in quantum systems. The -dimensional depolarizing channel can be viewed as a completely positive trace-preserving map , depending on one parameter , which maps a state onto a linear combination of itself and the maximally mixed state,
Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used to analyze the motion of a system of discrete particles each with a finite number of degrees of freedom. Lagrangian field theory applies to continua and fields, which have an infinite number of degrees of freedom.
The min-entropy, in information theory, is the smallest of the Rényi family of entropies, corresponding to the most conservative way of measuring the unpredictability of a set of outcomes, as the negative logarithm of the probability of the most likely outcome. The various Rényi entropies are all equal for a uniform distribution, but measure the unpredictability of a nonuniform distribution in different ways. The min-entropy is never greater than the ordinary or Shannon entropy and that in turn is never greater than the Hartley or max-entropy, defined as the logarithm of the number of outcomes with nonzero probability.

The theory of causal fermion systems is an approach to describe fundamental physics. It provides a unification of the weak, the strong and the electromagnetic forces with gravity at the level of classical field theory. Moreover, it gives quantum mechanics as a limiting case and has revealed close connections to quantum field theory. Therefore, it is a candidate for a unified physical theory. Instead of introducing physical objects on a preexisting spacetime manifold, the general concept is to derive spacetime as well as all the objects therein as secondary objects from the structures of an underlying causal fermion system. This concept also makes it possible to generalize notions of differential geometry to the non-smooth setting. In particular, one can describe situations when spacetime no longer has a manifold structure on the microscopic scale. As a result, the theory of causal fermion systems is a proposal for quantum geometry and an approach to quantum gravity.
In quantum information theory and quantum optics, the Schrödinger–HJW theorem is a result about the realization of a mixed state of a quantum system as an ensemble of pure quantum states and the relation between the corresponding purifications of the density operators. The theorem is named after physicists and mathematicians Erwin Schrödinger, Lane P. Hughston, Richard Jozsa and William Wootters. The result was also found independently by Nicolas Gisin, and by Nicolas Hadjisavvas building upon work by Ed Jaynes, while a significant part of it was likewise independently discovered by N. David Mermin. Thanks to its complicated history, it is also known by various other names such as the GHJW theorem, the HJW theorem, and the purification theorem.
In quantum information, the diamond norm, also known as completely bounded trace norm, is a norm on the space of quantum operations, or more generally on any linear map that acts on complex matrices. Its main application is to measure the "single use distinguishability" of two quantum channels. If an agent is randomly given one of two quantum channels, permitted to pass one state through the unknown channel, and then measures the state in an attempt to determine which operation they were given, then their maximal probability of success is determined by the diamond norm of the difference of the two channels.































































































