In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties that are used to distinguish topological spaces.

In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.
In the mathematical field of algebraic topology, the fundamental group of a topological space is the group of the equivalence classes under homotopy of the loops contained in the space. It records information about the basic shape, or holes, of the topological space. The fundamental group is the first and simplest homotopy group. The fundamental group is a homotopy invariant—topological spaces that are homotopy equivalent have isomorphic fundamental groups. The fundamental group of a topological space is denoted by .
In mathematics, a topological space is called separable if it contains a countable, dense subset; that is, there exists a sequence of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology.

In mathematics, topological groups are the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two structures together and consequently they are not independent from each other.
In mathematics, homology is a general way of associating a sequence of algebraic objects, such as abelian groups or modules, with other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topology. Similar constructions are available in a wide variety of other contexts, such as abstract algebra, groups, Lie algebras, Galois theory, and algebraic geometry.

In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology.

In topology and related areas of mathematics, the quotient space of a topological space under a given equivalence relation is a new topological space constructed by endowing the quotient set of the original topological space with the quotient topology, that is, with the finest topology that makes continuous the canonical projection map. In other words, a subset of a quotient space is open if and only if its preimage under the canonical projection map is open in the original topological space.
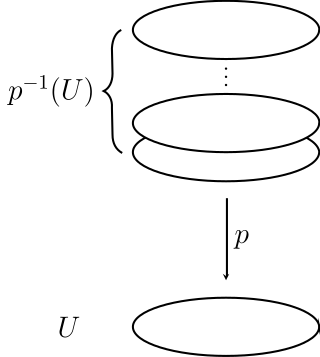
In topology, a covering or covering projection is a map between topological spaces that, intuitively, locally acts like a projection of multiple copies of a space onto itself. In particular, coverings are special types of local homeomorphisms. If is a covering, is said to be a covering space or cover of , and is said to be the base of the covering, or simply the base. By abuse of terminology, and may sometimes be called covering spaces as well. Since coverings are local homeomorphisms, a covering space is a special kind of étale space.
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, denoted which records information about loops in a space. Intuitively, homotopy groups record information about the basic shape, or holes, of a topological space.
A CW complex is a kind of a topological space that is particularly important in algebraic topology. It was introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial nature that allows for computation. The C stands for "closure-finite", and the W for "weak" topology.
In mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed. It is the smallest example of a topological space which is neither trivial nor discrete. It is named after Wacław Sierpiński.
In mathematics, specifically in homotopy theory, a classifying spaceBG of a topological group G is the quotient of a weakly contractible space EG by a proper free action of G. It has the property that any G principal bundle over a paracompact manifold is isomorphic to a pullback of the principal bundle . As explained later, this means that classifying spaces represent a set-valued functor on the homotopy category of topological spaces. The term classifying space can also be used for spaces that represent a set-valued functor on the category of topological spaces, such as Sierpiński space. This notion is generalized by the notion of classifying topos. However, the rest of this article discusses the more commonly used notion of classifying space up to homotopy.

In mathematics, a path in a topological space is a continuous function from a closed interval into

In mathematics, triangulation describes the replacement of topological spaces by piecewise linear spaces, i.e. the choice of a homeomorphism in a suitable simplicial complex. Spaces being homeomorphic to a simplicial complex are called triangulable. Triangulation has various uses in different branches of mathematics, for instance in algebraic topology, in complex analysis or in modeling.
In topology, a branch of mathematics, a retraction is a continuous mapping from a topological space into a subspace that preserves the position of all points in that subspace. The subspace is then called a retract of the original space. A deformation retraction is a mapping that captures the idea of continuously shrinking a space into a subspace.
In algebraic topology, homotopical connectivity is a property describing a topological space based on the dimension of its holes. In general, low homotopical connectivity indicates that the space has at least one low-dimensional hole. The concept of n-connectedness generalizes the concepts of path-connectedness and simple connectedness.

In topology and other branches of mathematics, a topological space X is locally connected if every point admits a neighbourhood basis consisting of open connected sets.
This is a glossary of properties and concepts in algebraic topology in mathematics.