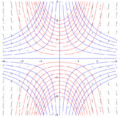
A slope field (also called a direction field [1] ) is a graphical representation of the solutions to a first-order differential equation [2] of a scalar function. Solutions to a slope field are functions drawn as solid curves. A slope field shows the slope of a differential equation at certain vertical and horizontal intervals on the x-y plane, and can be used to determine the approximate tangent slope at a point on a curve, where the curve is some solution to the differential equation.
Contents
- Definition
- Standard case
- General case of a system of differential equations
- General application
- Software for plotting slope fields
- Direction field code in GNU Octave/MATLAB
- Example code for Maxima
- Example code for Mathematica
- Example code for SageMath[4]
- Examples
- See also
- References
- Bibliography
- External links