
The Mandelbrot set is the set of complex numbers for which the function does not diverge to infinity when iterated from , i.e., for which the sequence , , etc., remains bounded in absolute value.

A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the centre of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

The Sierpiński triangle, also called the Sierpiński gasket or Sierpiński sieve, is a fractal attractive fixed set with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. Originally constructed as a curve, this is one of the basic examples of self-similar sets—that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries before the work of Sierpiński.

In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.

In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects.

In elementary geometry, two geometric objects are perpendicular if their intersection forms right angles at the point of intersection called a foot. The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. Perpendicular intersections can happen between two lines, between a line and a plane, and between two planes.

A shape or figure is a graphical representation of an object or its external boundary, outline, or external surface, as opposed to other properties such as color, texture, or material type. A plane shape or plane figure is constrained to lie on a plane, in contrast to solid 3D shapes. A two-dimensional shape or two-dimensional figure may lie on a more general curved surface.

In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in n-dimensional Euclidean space.

Stairs are a structure designed to bridge a large vertical distance between lower and higher levels by dividing it into smaller vertical distances. This is achieved as a diagonal series of horizontal platforms called steps which enable passage to the other level by stepping from one to another step in turn. Steps are very typically rectangular. Stairs may be straight, round, or may consist of two or more straight pieces connected at angles.
In electrical engineering, the distributed-element model or transmission-line model of electrical circuits assumes that the attributes of the circuit are distributed continuously throughout the material of the circuit. This is in contrast to the more common lumped-element model, which assumes that these values are lumped into electrical components that are joined by perfectly conducting wires. In the distributed-element model, each circuit element is infinitesimally small, and the wires connecting elements are not assumed to be perfect conductors; that is, they have impedance. Unlike the lumped-element model, it assumes nonuniform current along each branch and nonuniform voltage along each wire.

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n.

In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. It is a circular arc that measures 180°. It has only one line of symmetry. In non-technical usage, the term "semicircle" is sometimes used to refer to a half-disk, which is a two-dimensional geometric shape that also includes the diameter segment from one end of the arc to the other as well as all the interior points.

The Loretto Chapel in Santa Fe, New Mexico, United States, is a former Roman Catholic church that is now used as a museum and a wedding chapel.

The coastline paradox is the counterintuitive observation that the coastline of a landmass does not have a well-defined length. This results from the fractal curve-like properties of coastlines; i.e., the fact that a coastline typically has a fractal dimension. Although the "paradox of length" was previously noted by Hugo Steinhaus, the first systematic study of this phenomenon was by Lewis Fry Richardson, and it was expanded upon by Benoit Mandelbrot.

The Church of Our Saviour is a baroque church in Copenhagen, Denmark, most famous for the external spiral winding staircase that can be climbed to the top, offering extensive views over central Copenhagen. It is also noted for its carillon, which is the largest in northern Europe and plays melodies every hour from 8 am to midnight.
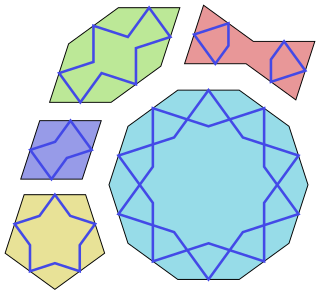
Girihtiles are a set of five tiles that were used in the creation of Islamic geometric patterns using strapwork (girih) for decoration of buildings in Islamic architecture. They have been used since about the year 1200 and their arrangements found significant improvement starting with the Darb-i Imam shrine in Isfahan in Iran built in 1453.

NGC 1672 is a barred spiral galaxy located in the constellation Dorado. It was discovered by the astronomer James Dunlop on November 5, 1826. It was originally unclear whether it was a member of the Dorado Group, with some sources finding it to be a member and other sources rejecting its membership. However, recent tip of the red-giant branch (TRGB) measurements indicate that NGC 1672 is located at the same distance as other members, suggesting it is indeed a member of the Dorado Group.

In fractal geometry, the H tree is a fractal tree structure constructed from perpendicular line segments, each smaller by a factor of the square root of 2 from the next larger adjacent segment. It is so called because its repeating pattern resembles the letter "H". It has Hausdorff dimension 2, and comes arbitrarily close to every point in a rectangle. Its applications include VLSI design and microwave engineering.

In geometry, two or more objects are said to be concentric when they share the same center. Any pair of objects with well-defined centers can be concentric, including circles, spheres, regular polygons, regular polyhedra, parallelograms, cones, conic sections, and quadrics.

In microwave systems, a spiral antenna is a type of RF antenna. It is shaped as a two-arm spiral, or more arms may be used. Spiral antennas were first described in 1956. Logarithmic spiral antennas belong to the class of frequency independent antennas; the driving point impedance, radiation pattern and polarization of such antennas remain unchanged over a large bandwidth range. Spiral antennas are inherently circularly polarized with low gain. Antenna arrays can be used to increase the gain. Spiral antennas are reduced size antennas with its windings making it an extremely small structure. Lossy cavities are usually placed at the back to eliminate back lobes because a unidirectional pattern is usually preferred in such antennas. Spiral antennas are classified into different types; Archimedean spiral, logarithmic spiral, square spiral, and star spiral, etc. Archimedean spiral is the most popular configuration.























