In Euclidean geometry, a splitter is a line segment through one of the vertices of a triangle (that is, a cevian) that bisects the perimeter of the triangle. [1] [2] They are not to be confused with cleavers, which also bisect the perimeter but instead emanate from the midpoint of one of the triangle's sides.
The opposite endpoint of a splitter to the chosen triangle vertex lies at the point on the triangle's side where one of the excircles of the triangle is tangent to that side. [1] [2] This point is also called a splitting point of the triangle. [2] It is additionally a vertex of the extouch triangle and one of the points where the Mandart inellipse is tangent to the triangle side. [3]
The three splitters concur at the Nagel point of the triangle, [1] which is also called its splitting center. [2]
Some authors have used the term "splitter" in a more general sense, for any line segment that bisects the perimeter of the triangle. Other line segments of this type include the cleavers, which are perimeter-bisecting segments that pass through the midpoint of a triangle side, and the equalizers, segments that bisect both the area and perimeter of a triangle. [4]
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle. The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. It can be defined between two lines, between a line and a plane, and between two planes.
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.
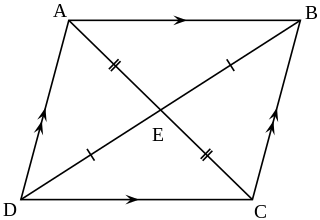
In Euclidean geometry, a parallelogram is a simple (non-self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations.
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector.
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.
In geometry, symmedians are three particular geometrical lines associated with every triangle. They are constructed by taking a median of the triangle, and reflecting the line over the corresponding angle bisector. The angle formed by the symmedian and the angle bisector has the same measure as the angle between the median and the angle bisector, but it is on the other side of the angle bisector.
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name. When the semiperimeter occurs as part of a formula, it is typically denoted by the letter s.
In geometry, lines in a plane or higher-dimensional space are said to be concurrent if they intersect at a single point. They are in contrast to parallel lines.
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".
In geometry, a cevian is a line that intersects both a triangle's vertex, and also the side that is opposite to that vertex. Medians and angle bisectors are special cases of cevians. The name "cevian" comes from the Italian mathematician Giovanni Ceva, who proved a well-known theorem about cevians which also bears his name.
In geometry, the Nagel point is a triangle center, one of the points associated with a given triangle whose definition does not depend on the placement or scale of the triangle. It is the point of concurrency of all three of the triangle's splitters.
In geometry, the incircle of the medial triangle of a triangle is the Spieker circle, named after 19th-century German geometer Theodor Spieker. Its center, the Spieker center, in addition to being the incenter of the medial triangle, is the center of mass of the uniform-density boundary of triangle. The Spieker center is also the point where all three cleavers of the triangle intersect each other.
In Euclidean geometry, a circumconic is a conic section that passes through the three vertices of a triangle, and an inconic is a conic section inscribed in the sides, possibly extended, of a triangle.
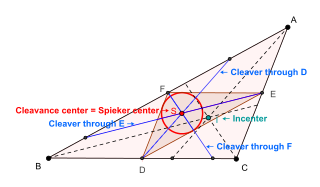
In geometry, a cleaver of a triangle is a line segment that bisects the perimeter of the triangle and has one endpoint at the midpoint of one of the three sides. They are not to be confused with splitters, which also bisect the perimeter, but with an endpoint on one of the triangle’s vertices instead of its sides.
In geometry, the Steiner inellipse, midpoint inellipse, or midpoint ellipse of a triangle is the unique ellipse inscribed in the triangle and tangent to the sides at their midpoints. It is an example of an inellipse. By comparison the inscribed circle and Mandart inellipse of a triangle are other inconics that are tangent to the sides, but not at the midpoints unless the triangle is equilateral. The Steiner inellipse is attributed by Dörrie to Jakob Steiner, and a proof of its uniqueness is given by Dan Kalman.
In geometry, the Spieker center is a special point associated with a plane triangle. It is defined as the center of mass of the perimeter of the triangle. The Spieker center of a triangle △ABC is the center of gravity of a homogeneous wire frame in the shape of △ABC. The point is named in honor of the 19th-century German geometer Theodor Spieker. The Spieker center is a triangle center and it is listed as the point X(10) in Clark Kimberling's Encyclopedia of Triangle Centers.
In plane geometry, an extended side or sideline of a polygon is the line that contains one side of the polygon. The extension of a side arises in various contexts.