
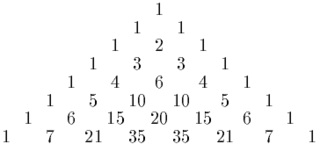
The Star of David theorem is a mathematical result on arithmetic properties of binomial coefficients. It was discovered by Henry W. Gould in 1972.

The Star of David theorem is a mathematical result on arithmetic properties of binomial coefficients. It was discovered by Henry W. Gould in 1972.
The greatest common divisors of the binomial coefficients forming each of the two triangles in the Star of David shape in Pascal's triangle are equal:
Rows 8, 9, and 10 of Pascal's triangle are
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | ||||||||||||||
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | |||||||||||||
| 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |
For n=9, k=3 or n=9, k=6, the element 84 is surrounded by, in sequence, the elements 28, 56, 126, 210, 120, 36. Taking alternating values, we have gcd(28, 126, 120) = 2 = gcd(56, 210, 36).
The element 36 is surrounded by the sequence 8, 28, 84, 120, 45, 9, and taking alternating values we have gcd(8, 84, 45) = 1 = gcd(28, 120, 9).
The above greatest common divisor also equals [1] Thus in the above example for the element 84 (in its rightmost appearance), we also have gcd(70, 56, 28, 8) = 2. This result in turn has further generalizations.
The two sets of three numbers which the Star of David theorem says have equal greatest common divisors also have equal products. [1] For example, again observing that the element 84 is surrounded by, in sequence, the elements 28, 56, 126, 210, 120, 36, and again taking alternating values, we have 28×126×120 = 26×33×5×72 = 56×210×36. This result can be confirmed by writing out each binomial coefficient in factorial form, using

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written It is the coefficient of the xk term in the polynomial expansion of the binomial power (1 + x)n, and is given by the formula
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. For example,
In elementary number theory, Bézout's identity is the following theorem:
In mathematics, a combination is a selection of items from a collection, such that the order of selection does not matter. For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S. If the set has n elements, the number of k-combinations is equal to the binomial coefficient

In arithmetic and number theory, the least common multiple, lowest common multiple, or smallest common multiple of two integers a and b, usually denoted by lcm(a, b), is the smallest positive integer that is divisible by both a and b. Since division of integers by zero is undefined, this definition has meaning only if a and b are both different from zero. However, some authors define lcm(a,0) as 0 for all a, which is the result of taking the lcm to be the least upper bound in the lattice of divisibility.
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in India, Persia, China, Germany, and Italy.
In mathematics, a unique factorization domain (UFD) is a ring in which a statement analogous to the fundamental theorem of arithmetic holds. Specifically, a UFD is an integral domain in which every non-zero non-unit element can be written as a product of prime elements, uniquely up to order and units.
In arithmetic and computer programming, the extended Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common divisor (gcd) of integers a and b, also the coefficients of Bézout's identity, which are integers x and y such that
In mathematics, the falling factorial is defined as the polynomial
In mathematics, a multiset is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements. The number of instances given for each element is called the multiplicity of that element in the multiset. As a consequence, an infinite number of multisets exist which contain only elements a and b, but vary in the multiplicities of their elements:
In mathematics, the multinomial theorem describes how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem from binomials to multinomials.

A pentatope number is a number in the fifth cell of any row of Pascal's triangle starting with the 5-term row 1 4 6 4 1, either from left to right or from right to left.
In mathematics, the Gaussian binomial coefficients are q-analogs of the binomial coefficients. The Gaussian binomial coefficient, written as or , is a polynomial in q with integer coefficients, whose value when q is set to a prime power counts the number of subspaces of dimension k in a vector space of dimension n over a finite field with q elements.
In mathematics, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1. Typically, mathematicians are interested in q-analogs that arise naturally, rather than in arbitrarily contriving q-analogs of known results. The earliest q-analog studied in detail is the basic hypergeometric series, which was introduced in the 19th century.
In mathematics the nth central binomial coefficient is the particular binomial coefficient
Singmaster's conjecture is a conjecture in combinatorial number theory in mathematics, named after the British mathematician David Singmaster who proposed it in 1971. It says that there is a finite upper bound on the multiplicities of entries in Pascal's triangle. It is clear that the only number that appears infinitely many times in Pascal's triangle is 1, because any other number x can appear only within the first x + 1 rows of the triangle.
In algebra, the content of a polynomial with integer coefficients is the greatest common divisor of its coefficients. The primitive part of such a polynomial is the quotient of the polynomial by its content. Thus a polynomial is the product of its primitive part and its content, and this factorization is unique up to the multiplication of the content by a unit of the ring of the coefficients.
In the context of combinatorial mathematics, stars and bars is a graphical aid for deriving certain combinatorial theorems. It was popularized by William Feller in his classic book on probability. It can be used to solve many simple counting problems, such as how many ways there are to put n indistinguishable balls into k distinguishable bins.
In combinatorial mathematics and statistics, the Fuss–Catalan numbers are numbers of the form
In mathematics, Bhargava's factorial function, or simply Bhargava factorial, is a certain generalization of the factorial function developed by the Fields Medal winning mathematician Manjul Bhargava as part of his thesis in Harvard University in 1996. The Bhargava factorial has the property that many number-theoretic results involving the ordinary factorials remain true even when the factorials are replaced by the Bhargava factorials. Using an arbitrary infinite subset S of the set Z of integers, Bhargava associated a positive integer with every positive integer k, which he denoted by k !S, with the property that if one takes S = Z itself, then the integer associated with k, that is k !Z, would turn out to be the ordinary factorial of k.