Str8ts is a logic-based number-placement puzzle, invented by Jeff Widderich in 2008. [1] It is distinct from, but shares some properties and rules with, Sudoku. The name is derived from the poker straight. The puzzle is published in a number of newspapers internationally, [2] in two book collections, and in downloadable apps. It was featured on the Canadian television show Dragons' Den on November 24, 2010.
A hand made prototype of Str8ts which used black cells and the new rule of straights in compartments was invented by Canadian puzzle designer Jeff Widderich in 2007. He approached Andrew Stuart, a UK-based puzzle maker and programmer, to make the puzzle. Their collaboration settled how the clues would be determined and finalized the rules. The first puzzle was presented at the Nuremberg International Toy Fair in February 2008. A daily puzzle has been published at their website since 24 November 2008, and more recently, a weekly "extreme" puzzle has appeared, which incorporates an active discussion forum for each puzzle. The puzzle has appeared in Süddeutsche Zeitung since March 2010, and in the Saturday edition of Die Rheinpfalz since August 2010. An iOS app was released in July 2009, containing hundreds of puzzles in four difficulty levels. [3]
In August 2010, a wooden board and piece version was designed by Intellego holzspiele. [4] Widderich appeared with the game in the fifth season of the Canadian television show Dragons' Den on November 24, 2010, where he made a deal for a $150,000 investment in return for 10% royalties, from three of the panelists. [5] [6] [7]
The solver is given a 9x9 grid, partially divided by black cells into compartments. Each compartment, vertically or horizontally, must contain a straight – a set of consecutive numbers, but in any order. For example: 7, 6, 4, 5 is valid, but 1, 3, 8, 7 is not.
Like Sudoku, the solver must fill the remaining white cells with numbers 1 to 9 (or 1 to n in puzzles with N cells per side) such that each row and column contains unique digits. Whereas Sudoku has the additional constraint of 3x3 boxes, in Str8ts rows and columns are divided by blacks cells. Additional clues are set in some of the black cells – these numbers remove that digit as an option in the row and column. Such digits do not form part of any straight.
There are a number of variants to the basic game, including Symmetric Str8ts, Asymmetric Str8ts, Mini-Str8ts, and Transformations.
As Str8ts belongs to the same class of puzzles as Sudoku the puzzle can demonstrate a wide spectrum of relative difficulty. The grade is determined by a combination of opportunities to solve at each stage and the difficulty of the strategy that grants each solution. An easier puzzle will have many places where a logical deduction can place a solution or eliminate a candidate number. When the whole puzzle is assessed in this way, plus some heuristics, a score can be determined. Over a large number of puzzles (>10,000) a bell curve of scores can be produced. This can be quartiled to group puzzles into specific grades. [8]
The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other; thus, a solution requires that no two queens share the same row, column, or diagonal. There are 92 solutions. The problem was first posed in the mid-19th century. In the modern era, it is often used as an example problem for various computer programming techniques.
Nonograms, also known as Hanjie, Paint by Numbers, Picross, Griddlers, and Pic-a-Pix are picture logic puzzles in which cells in a grid must be colored or left blank according to numbers at the edges of the grid to reveal a hidden picture. In this puzzle, the numbers are a form of discrete tomography that measures how many unbroken lines of filled-in squares there are in any given row or column. For example, a clue of "4 8 3" would mean there are sets of four, eight, and three filled squares, in that order, with at least one blank square between successive sets.
Verbal arithmetic, also known as alphametics, cryptarithmetic, cryptarithm or word addition, is a type of mathematical game consisting of a mathematical equation among unknown numbers, whose digits are represented by letters of the alphabet. The goal is to identify the value of each letter. The name can be extended to puzzles that use non-alphabetic symbols instead of letters.
Kakuro or Kakkuro or Kakoro is a kind of logic puzzle that is often referred to as a mathematical transliteration of the crossword. Kakuro puzzles are regular features in many math-and-logic puzzle publications across the world. In 1966, Canadian Jacob E. Funk, an employee of Dell Magazines, came up with the original English name Cross Sums and other names such as Cross Addition have also been used, but the Japanese name Kakuro, abbreviation of Japanese kasan kurosu, seems to have gained general acceptance and the puzzles appear to be titled this way now in most publications. The popularity of Kakuro in Japan is immense, second only to Sudoku among Nikoli's famed logic-puzzle offerings.
Sudoku is a logic-based, combinatorial number-placement puzzle. In classic Sudoku, the objective is to fill a 9 × 9 grid with digits so that each column, each row, and each of the nine 3 × 3 subgrids that compose the grid contains all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution.
Hitori is a type of logic puzzle published by Nikoli.
In the mathematical field of combinatorics, given a collection of subsets of a set , an exact cover is a subcollection of such that each element in is contained in exactly one subset in . One says that each element in is covered by exactly one subset in . An exact cover is a kind of cover.
Mathematics can be used to study Sudoku puzzles to answer questions such as "How many filled Sudoku grids are there?", "What is the minimal number of clues in a valid puzzle?" and "In what ways can Sudoku grids be symmetric?" through the use of combinatorics and group theory.
Killer sudoku is a puzzle that combines elements of sudoku and kakuro. Despite the name, the simpler killer sudokus can be easier to solve than regular sudokus, depending on the solver's skill at mental arithmetic; the hardest ones, however, can take hours to solve.
This is a glossary of Sudoku terms and jargon. It is organized thematically, with links to references and example usage provided as ([1]). Sudoku with a 9×9 grid is assumed, unless otherwise noted.
Inshi no heya is a type of logic puzzle published by Nikoli. It is a specific form of the KenKen puzzle genre where every operation is implied to be multiplication.
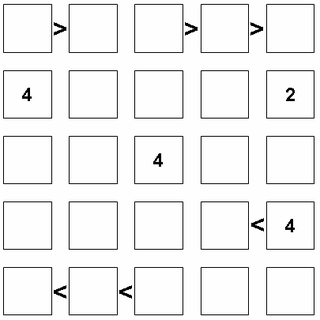
Futoshiki, or More or Less, is a logic puzzle game from Japan. Its name means "inequality". It is also spelled hutosiki. Futoshiki was developed by Tamaki Seto in 2001.
A standard Sudoku contains 81 cells, in a 9×9 grid, and has 9 boxes, each box being the intersection of the first, middle, or last 3 rows, and the first, middle, or last 3 columns. Each cell may contain a number from one to nine, and each number can only occur once in each row, column, and box. A Sudoku starts with some cells containing numbers (clues), and the goal is to solve the remaining cells. Proper Sudokus have one solution. Players and investigators use a wide range of computer algorithms to solve Sudokus, study their properties, and make new puzzles, including Sudokus with interesting symmetries and other properties.
A Survo puzzle is a kind of logic puzzle presented and studied by Seppo Mustonen. The name of the puzzle is associated with Mustonen's Survo system, which is a general environment for statistical computing and related areas.
KenKen and KenDoku are trademarked names for a style of arithmetic and logic puzzle invented in 2004 by Japanese math teacher Tetsuya Miyamoto, who intended the puzzles to be an instruction-free method of training the brain. The name derives from the Japanese word for cleverness. The names Calcudoku and Mathdoku are sometimes used by those who do not have the rights to use the KenKen or KenDoku trademarks.
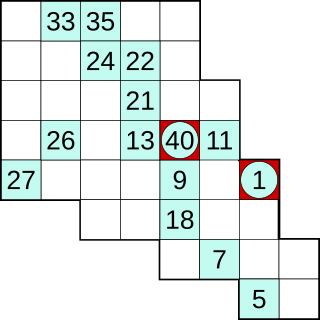
Hidato, also known as "Hidoku", is a logic puzzle game invented by Dr. Gyora M. Benedek, an Israeli mathematician. The goal of Hidato is to fill the grid with consecutive numbers that connect horizontally, vertically, or diagonally. The name Hidato is a registered trademark. Some publishers use different names for this puzzle such as Number Snake, Snakepit, Jadium or Numbrix.
Minesweeper is a logic puzzle video game genre generally played on personal computers. The game features a grid of clickable tiles, with hidden "mines" scattered throughout the board. The objective is to clear the board without detonating any mines, with help from clues about the number of neighboring mines in each field. Variants of Minesweeper have been made that expand on the basic concepts, such as Minesweeper X, Crossmines, and Minehunt. Minesweeper has been incorporated as a minigame in other games, such as RuneScape and Minecraft's 2015 April Fools update.
Takuzu, also known as Binairo, is a logic puzzle involving placement of two symbols, often 1s and 0s, on a rectangular grid. The objective is to fill the grid with 1s and 0s, where there is an equal number of 1s and 0s in each row and column and no more than two of either number adjacent to each other. Additionally, there can be no identical rows or columns. Similar to Sudoku, each puzzle begins with several squares in the grid already filled.
In the mathematics of Sudoku, the Sudoku graph is an undirected graph whose vertices represent the cells of a (blank) Sudoku puzzle and whose edges represent pairs of cells that belong to the same row, column, or block of the puzzle. The problem of solving a Sudoku puzzle can be represented as precoloring extension on this graph. It is an integral Cayley graph.
Taking Sudoku Seriously: The math behind the world's most popular pencil puzzle is a book on the mathematics of Sudoku. It was written by Jason Rosenhouse and Laura Taalman, and published in 2011 by the Oxford University Press. The Basic Library List Committee of the Mathematical Association of America has suggested its inclusion in undergraduate mathematics libraries. It was the 2012 winner of the PROSE Awards in the popular science and popular mathematics category.