Related Research Articles
Causality is influence by which one event, process, state, or object contributes to the production of another event, process, state, or object where the cause is partly responsible for the effect, and the effect is partly dependent on the cause. In general, a process has many causes, which are also said to be causal factors for it, and all lie in its past. An effect can in turn be a cause of, or causal factor for, many other effects, which all lie in its future. Some writers have held that causality is metaphysically prior to notions of time and space.
The phrase "correlation does not imply causation" refers to the inability to legitimately deduce a cause-and-effect relationship between two events or variables solely on the basis of an observed association or correlation between them. The idea that "correlation implies causation" is an example of a questionable-cause logical fallacy, in which two events occurring together are taken to have established a cause-and-effect relationship. This fallacy is also known by the Latin phrase cum hoc ergo propter hoc. This differs from the fallacy known as post hoc ergo propter hoc, in which an event following another is seen as a necessary consequence of the former event, and from conflation, the errant merging of two events, ideas, databases, etc., into one.
Ceteris paribus or caeteris paribus is a Latin phrase meaning "other things equal"; English translations of the phrase include "all other things being equal" or "other things held constant" or "all else unchanged". A prediction or a statement about a causal, empirical, or logical relation between two states of affairs is ceteris paribus if it is acknowledged that the prediction, although usually accurate in expected conditions, can fail or the relation can be abolished by intervening factors.

In statistics, an interaction may arise when considering the relationship among three or more variables, and describes a situation in which the effect of one causal variable on an outcome depends on the state of a second causal variable. Although commonly thought of in terms of causal relationships, the concept of an interaction can also describe non-causal associations. Interactions are often considered in the context of regression analyses or factorial experiments.

In statistics, a spurious relationship or spurious correlation is a mathematical relationship in which two or more events or variables are associated but not causally related, due to either coincidence or the presence of a certain third, unseen factor.
In statistics, econometrics, epidemiology and related disciplines, the method of instrumental variables (IV) is used to estimate causal relationships when controlled experiments are not feasible or when a treatment is not successfully delivered to every unit in a randomized experiment. Intuitively, IVs are used when an explanatory variable of interest is correlated with the error term, in which case ordinary least squares and ANOVA give biased results. A valid instrument induces changes in the explanatory variable but has no independent effect on the dependent variable, allowing a researcher to uncover the causal effect of the explanatory variable on the dependent variable.
Internal validity is the extent to which a piece of evidence supports a claim about cause and effect, within the context of a particular study. It is one of the most important properties of scientific studies and is an important concept in reasoning about evidence more generally. Internal validity is determined by how well a study can rule out alternative explanations for its findings. It contrasts with external validity, the extent to which results can justify conclusions about other contexts.
External validity is the validity of applying the conclusions of a scientific study outside the context of that study. In other words, it is the extent to which the results of a study can be generalized to and across other situations, people, stimuli, and times. In contrast, internal validity is the validity of conclusions drawn within the context of a particular study. Because general conclusions are almost always a goal in research, external validity is an important property of any study. Mathematical analysis of external validity concerns a determination of whether generalization across heterogeneous populations is feasible, and devising statistical and computational methods that produce valid generalizations.
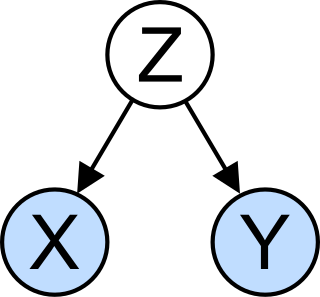
In statistics, a confounder is a variable that influences both the dependent variable and independent variable, causing a spurious association. Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations. The existence of confounders is an important quantitative explanation why correlation does not imply causation.
The Rubin causal model (RCM), also known as the Neyman–Rubin causal model, is an approach to the statistical analysis of cause and effect based on the framework of potential outcomes, named after Donald Rubin. The name "Rubin causal model" was first coined by Paul W. Holland. The potential outcomes framework was first proposed by Jerzy Neyman in his 1923 Master's thesis, though he discussed it only in the context of completely randomized experiments. Rubin extended it into a general framework for thinking about causation in both observational and experimental studies.
In the philosophy of science, a causal model is a conceptual model that describes the causal mechanisms of a system. Causal models can improve study designs by providing clear rules for deciding which independent variables need to be included/controlled for.

In statistics, a mediation model seeks to identify and explain the mechanism or process that underlies an observed relationship between an independent variable and a dependent variable via the inclusion of a third hypothetical variable, known as a mediator variable. Rather than a direct causal relationship between the independent variable and the dependent variable, a mediation model proposes that the independent variable influences the mediator variable, which in turn influences the dependent variable. Thus, the mediator variable serves to clarify the nature of the relationship between the independent and dependent variables.
In causal models, controlling for a variable means binning data according to measured values of the variable. This is typically done so that the variable can no longer act as a confounder in, for example, an observational study or experiment.

In epidemiology, Mendelian randomization is a method using measured variation in genes to interrogate the causal effect of an exposure on an outcome. Under key assumptions, the design reduces both reverse causation and confounding, which often substantially impede or mislead the interpretation of results from epidemiological studies.
The average treatment effect (ATE) is a measure used to compare treatments in randomized experiments, evaluation of policy interventions, and medical trials. The ATE measures the difference in mean (average) outcomes between units assigned to the treatment and units assigned to the control. In a randomized trial, the average treatment effect can be estimated from a sample using a comparison in mean outcomes for treated and untreated units. However, the ATE is generally understood as a causal parameter that a researcher desires to know, defined without reference to the study design or estimation procedure. Both observational studies and experimental study designs with random assignment may enable one to estimate an ATE in a variety of ways.
In the statistical analysis of observational data, propensity score matching (PSM) is a statistical matching technique that attempts to estimate the effect of a treatment, policy, or other intervention by accounting for the covariates that predict receiving the treatment. PSM attempts to reduce the bias due to confounding variables that could be found in an estimate of the treatment effect obtained from simply comparing outcomes among units that received the treatment versus those that did not. Paul R. Rosenbaum and Donald Rubin introduced the technique in 1983.
Causal reasoning is the process of identifying causality: the relationship between a cause and its effect. The study of causality extends from ancient philosophy to contemporary neuropsychology; assumptions about the nature of causality may be shown to be functions of a previous event preceding a later one. The first known protoscientific study of cause and effect occurred in Aristotle's Physics. Causal inference is an example of causal reasoning.
Causal inference is the process of determining the independent, actual effect of a particular phenomenon that is a component of a larger system. The main difference between causal inference and inference of association is that causal inference analyzes the response of an effect variable when a cause of the effect variable is changed. The science of why things occur is called etiology. Causal inference is said to provide the evidence of causality theorized by causal reasoning.
In statistics, Lord's paradox raises the issue of when it is appropriate to control for baseline status. In three papers, Frederic M. Lord gave examples when statisticians could reach different conclusions depending on whether they adjust for pre-existing differences. Holland & Rubin (1983) use these examples to illustrate how there may be multiple valid descriptive comparisons in the data, but causal conclusions require an underlying (untestable) causal model.

The Book of Why: The New Science of Cause and Effect is a 2018 nonfiction book by computer scientist Judea Pearl and writer Dana Mackenzie. The book explores the subject of causality and causal inference from statistical and philosophical points of view for a general audience.
References
- ↑ Krus, D. J., & Wilkinson, S. M. (1986). Demonstration of properties of a suppressor variable. Behavior Research Methods, Instruments, & Computers, 18(1), 21-24.