In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra.

A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. The triangle's interior is a two-dimensional region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex.
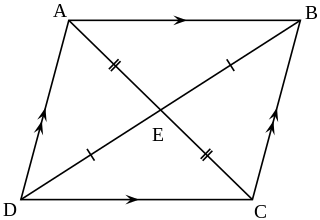
In Euclidean geometry, a parallelogram is a simple (non-self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations.

In geometry, bisection is the division of something into two equal or congruent parts. Usually it involves a bisecting line, also called a bisector. The most often considered types of bisectors are the segment bisector, a line that passes through the midpoint of a given segment, and the angle bisector, a line that passes through the apex of an angle . In three-dimensional space, bisection is usually done by a bisecting plane, also called the bisector.

In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the side opposite the vertex. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ∠ ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

In geometry, the Lemoine point, Grebe point or symmedian point is the intersection of the three symmedians of a triangle.

In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangle's centroid. In the case of isosceles and equilateral triangles, a median bisects any angle at a vertex whose two adjacent sides are equal in length. The concept of a median extends to tetrahedra.
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center.

In geometry, the isogonal conjugate of a point P with respect to a triangle △ABC is constructed by reflecting the lines PA, PB, PC about the angle bisectors of A, B, C respectively. These three reflected lines concur at the isogonal conjugate of P. This is a direct result of the trigonometric form of Ceva's theorem.

In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. The line through these points is the Simson line of P, named for Robert Simson. The concept was first published, however, by William Wallace in 1799, and is sometimes called the Wallace line.

In geometry, Brocard points are special points within a triangle. They are named after Henri Brocard (1845–1922), a French mathematician.
In geometry, the isotomic conjugate of a point P with respect to a triangle △ABC is another point, defined in a specific way from P and △ABC: If the base points of the lines PA, PB, PC on the sides opposite A, B, C are reflected about the midpoints of their respective sides, the resulting lines intersect at the isotomic conjugate of P.
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.
In Euclidean geometry, trilinear polarity is a certain correspondence between the points in the plane of a triangle not lying on the sides of the triangle and lines in the plane of the triangle not passing through the vertices of the triangle. "Although it is called a polarity, it is not really a polarity at all, for poles of concurrent lines are not collinear points." It was Jean-Victor Poncelet (1788–1867), a French engineer and mathematician, who introduced the idea of the trilinear polar of a point in 1865.
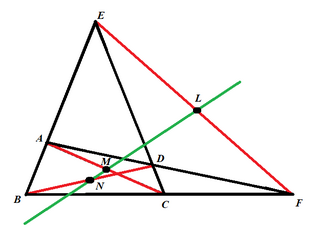
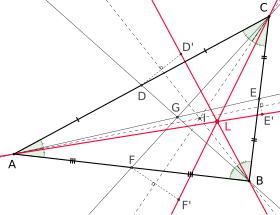
In geometry, the Newton–Gauss line is the line joining the midpoints of the three diagonals of a complete quadrilateral.
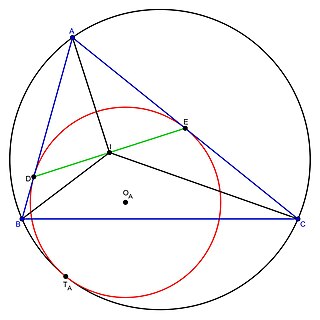
In plane geometry, a mixtilinear incircle of a triangle is a circle which is tangent to two of its sides and internally tangent to its circumcircle. The mixtilinear incircle of a triangle tangent to the two sides containing vertex is called the -mixtilinear incircle. Every triangle has three unique mixtilinear incircles, one corresponding to each vertex.

In mathematics, modern triangle geometry, or new triangle geometry, is the body of knowledge relating to the properties of a triangle discovered and developed roughly since the beginning of the last quarter of the nineteenth century. Triangles and their properties were the subject of investigation since at least the time of Euclid. In fact, Euclid's Elements contains description of the four special points – centroid, incenter, circumcenter and orthocenter - associated with a triangle. Even though Pascal and Ceva in the seventeenth century, Euler in the eighteenth century and Feuerbach in the nineteenth century and many other mathematicians had made important discoveries regarding the properties of the triangle, it was the publication in 1873 of a paper by Emile Lemoine (1840–1912) with the title "On a remarkable point of the triangle" that was considered to have, according to Nathan Altschiller-Court, "laid the foundations...of the modern geometry of the triangle as a whole." The American Mathematical Monthly, in which much of Lemoine's work is published, declared that "To none of these [geometers] more than Émile-Michel-Hyacinthe Lemoine is due the honor of starting this movement of modern triangle geometry". The publication of this paper caused a remarkable upsurge of interest in investigating the properties of the triangle during the last quarter of the nineteenth century and the early years of the twentieth century. A hundred-page article on triangle geometry in Klein's Encyclopedia of Mathematical Sciences published in 1914 bears witness to this upsurge of interest in triangle geometry.