Talbot effect

Last updated
The optical Talbot effect for monochromatic light, shown as a "Talbot carpet". At the bottom of the figure the light can be seen diffracting through a grating, and this pattern is reproduced at the top of the picture (one Talbot length away from the grating). At regular fractions of the Talbot length the sub-images form. Talbot carpet.png
The optical Talbot effect for monochromatic light, shown as a "Talbot carpet". At the bottom of the figure the light can be seen diffracting through a grating, and this pattern is reproduced at the top of the picture (one Talbot length away from the grating). At regular fractions of the Talbot length the sub-images form.

The Talbot effect is a diffraction effect first observed in 1836 by Henry Fox Talbot. [1] When a plane wave is incident upon a periodic diffraction grating, the image of the grating is repeated at regular distances away from the grating plane. The regular distance is called the Talbot length, and the repeated images are called self images or Talbot images. Furthermore, at half the Talbot length, a self-image also occurs, but phase-shifted by half a period (the physical meaning of this is that it is laterally shifted by half the width of the grating period). At smaller regular fractions of the Talbot length, sub-images can also be observed. At one quarter of the Talbot length, the self-image is halved in size, and appears with half the period of the grating (thus twice as many images are seen). At one eighth of the Talbot length, the period and size of the images is halved again, and so forth creating a fractal pattern of sub images with ever-decreasing size, often referred to as a Talbot carpet. [2] Talbot cavities are used for coherent beam combination of laser sets.

Contents

Calculation of the Talbot length

Lord Rayleigh showed that the Talbot effect was a natural consequence of Fresnel diffraction and that the Talbot length can be found by the following formula: [3]

where is the period of the diffraction grating and is the wavelength of the light incident on the grating. However, if wavelength is comparable to grating period , this expression may lead to errors in up to 100%. [4] In this case the exact expression derived by Lord Rayleigh should be used:

Fresnel number of the finite size Talbot grating

The number of Fresnel zones that form first Talbot self-image of the grating with period and transverse size is given by exact formula . [5] This result is obtained via exact evaluation of Fresnel-Kirchhoff integral in the near field at distance . [6]

The atomic Talbot effect

Due to the quantum mechanical wave nature of particles, diffraction effects have also been observed with atoms—effects which are similar to those in the case of light. Chapman et al. carried out an experiment in which a collimated beam of sodium atoms was passed through two diffraction gratings (the second used as a mask) to observe the Talbot effect and measure the Talbot length. [7] The beam had a mean velocity of 1000 m/s corresponding to a de Broglie wavelength of = 0.017 nm . Their experiment was performed with 200 and 300 nm gratings which yielded Talbot lengths of 4.7 and 10.6 mm respectively. This showed that for an atomic beam of constant velocity, by using , the atomic Talbot length can be found in the same manner.

Nonlinear Talbot effect

The nonlinear Talbot effect results from self-imaging of the generated periodic intensity pattern at the output surface of the periodically poled LiTaO3 crystal. Both integer and fractional nonlinear Talbot effects were investigated. [8]

In cubic nonlinear Schrödinger's equation , nonlinear Talbot effect of rogue waves is observed numerically. [9]

The nonlinear Talbot effect was also realized in linear, nonlinear and highly nonlinear surface gravity water waves. In the experiment, the group observed that higher frequency periodic patterns at the fractional Talbot distance disappear. Further increase in the wave steepness lead to deviations from the established nonlinear theory, unlike in the periodic revival that occurs in the linear and nonlinear regime regime, in highly nonlinear regimes the wave crests exhibit self acceleration, followed by self deceleration at half the Talbot distance, thus completing a smooth transition of the periodic pulse train by half a period. [10]

Applications of the optical Talbot effect

The optical Talbot effect can be used in imaging applications to overcome the diffraction limit (e.g. in structured illumination fluorescence microscopy). [11]

Moreover, its capacity to generate very fine patterns is also a powerful tool in Talbot lithography. [12]

The Talbot cavity is used for the phase-locking of the laser sets. [13]

In experimental fluid dynamics, the Talbot effect has been implemented in Talbot interferometry to measure displacements [14] [15] and temperature, [16] [17] and deployed with laser-induced fluorescence to reconstruct free surfaces in 3D, [18] and measure velocity. [19]

See also

Related Research Articles

<span class="mw-page-title-main">Diffraction</span> Phenomenon of the motion of waves

Diffraction is the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a secondary source of the propagating wave. Italian scientist Francesco Maria Grimaldi coined the word diffraction and was the first to record accurate observations of the phenomenon in 1660.

<span class="mw-page-title-main">Wave interference</span> Phenomenon resulting from the superposition of two waves

In physics, interference is a phenomenon in which two coherent waves are combined by adding their intensities or displacements with due consideration for their phase difference. The resultant wave may have greater intensity or lower amplitude if the two waves are in phase or out of phase, respectively. Interference effects can be observed with all types of waves, for example, light, radio, acoustic, surface water waves, gravity waves, or matter waves as well as in loudspeakers as electrical waves.

<span class="mw-page-title-main">Nonlinear optics</span> Branch of physics

Nonlinear optics (NLO) is the branch of optics that describes the behaviour of light in nonlinear media, that is, media in which the polarization density P responds non-linearly to the electric field E of the light. The non-linearity is typically observed only at very high light intensities (when the electric field of the light is >108 V/m and thus comparable to the atomic electric field of ~1011 V/m) such as those provided by lasers. Above the Schwinger limit, the vacuum itself is expected to become nonlinear. In nonlinear optics, the superposition principle no longer holds.

<span class="mw-page-title-main">Wavelength</span> Distance over which a waves shape repeats

In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats. In other words, it is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, troughs, or zero crossings. Wavelength is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns. The inverse of the wavelength is called the spatial frequency. Wavelength is commonly designated by the Greek letter lambda (λ). The term "wavelength" is also sometimes applied to modulated waves, and to the sinusoidal envelopes of modulated waves or waves formed by interference of several sinusoids.

<span class="mw-page-title-main">Diffraction grating</span> Optical component which splits light into several beams

In optics, a diffraction grating is an optical grating with a periodic structure that diffracts light into several beams traveling in different directions. The emerging coloration is a form of structural coloration. The directions or diffraction angles of these beams depend on the wave (light) incident angle to the diffraction grating, the spacing or distance between adjacent diffracting elements on the grating, and the wavelength of the incident light. The grating acts as a dispersive element. Because of this, diffraction gratings are commonly used in monochromators and spectrometers, but other applications are also possible such as optical encoders for high-precision motion control and wavefront measurement.

<span class="mw-page-title-main">Angular resolution</span> Ability of any image-forming device to distinguish small details of an object

Angular resolution describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object, thereby making it a major determinant of image resolution. It is used in optics applied to light waves, in antenna theory applied to radio waves, and in acoustics applied to sound waves. The colloquial use of the term "resolution" sometimes causes confusion; when an optical system is said to have a high resolution or high angular resolution, it means that the perceived distance, or actual angular distance, between resolved neighboring objects is small. The value that quantifies this property, θ, which is given by the Rayleigh criterion, is low for a system with a high resolution. The closely related term spatial resolution refers to the precision of a measurement with respect to space, which is directly connected to angular resolution in imaging instruments. The Rayleigh criterion shows that the minimum angular spread that can be resolved by an image forming system is limited by diffraction to the ratio of the wavelength of the waves to the aperture width. For this reason, high resolution imaging systems such as astronomical telescopes, long distance telephoto camera lenses and radio telescopes have large apertures.

In many areas of science, Bragg's law, Wulff–Bragg's condition or Laue–Bragg interference, are a special case of Laue diffraction, giving the angles for coherent scattering of waves from a large crystal lattice. It describes how the superposition of wave fronts scattered by lattice planes leads to a strict relation between the wavelength and scattering angle. This law was initially formulated for X-rays, but it also applies to all types of matter waves including neutron and electron waves if there are a large number of atoms, as well as visible light with artificial periodic microscale lattices.

In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when plane waves are incident on a diffracting object, and the diffraction pattern is viewed at a sufficiently long distance from the object, and also when it is viewed at the focal plane of an imaging lens. In contrast, the diffraction pattern created near the diffracting object and is given by the Fresnel diffraction equation.

<span class="mw-page-title-main">Nonlinear Schrödinger equation</span> Nonlinear form of the Schrödinger equation

In theoretical physics, the (one-dimensional) nonlinear Schrödinger equation (NLSE) is a nonlinear variation of the Schrödinger equation. It is a classical field equation whose principal applications are to the propagation of light in nonlinear optical fibers and planar waveguides and to Bose–Einstein condensates confined to highly anisotropic, cigar-shaped traps, in the mean-field regime. Additionally, the equation appears in the studies of small-amplitude gravity waves on the surface of deep inviscid (zero-viscosity) water; the Langmuir waves in hot plasmas; the propagation of plane-diffracted wave beams in the focusing regions of the ionosphere; the propagation of Davydov's alpha-helix solitons, which are responsible for energy transport along molecular chains; and many others. More generally, the NLSE appears as one of universal equations that describe the evolution of slowly varying packets of quasi-monochromatic waves in weakly nonlinear media that have dispersion. Unlike the linear Schrödinger equation, the NLSE never describes the time evolution of a quantum state. The 1D NLSE is an example of an integrable model.

Self-phase modulation (SPM) is a nonlinear optical effect of light–matter interaction. An ultrashort pulse of light, when travelling in a medium, will induce a varying refractive index of the medium due to the optical Kerr effect. This variation in refractive index will produce a phase shift in the pulse, leading to a change of the pulse's frequency spectrum.

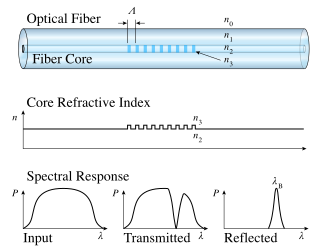
<span class="mw-page-title-main">Fiber Bragg grating</span> Type of distributed Bragg reflector constructed in a short segment of optical fiber

A fiber Bragg grating (FBG) is a type of distributed Bragg reflector constructed in a short segment of optical fiber that reflects particular wavelengths of light and transmits all others. This is achieved by creating a periodic variation in the refractive index of the fiber core, which generates a wavelength-specific dielectric mirror. Hence a fiber Bragg grating can be used as an inline optical filter to block certain wavelengths, can be used for sensing applications, or it can be used as wavelength-specific reflector.

In nonlinear optics, filament propagation is propagation of a beam of light through a medium without diffraction. This is possible because the Kerr effect causes an index of refraction change in the medium, resulting in self-focusing of the beam.

<span class="mw-page-title-main">Rayleigh length</span> Concept in laser optics

In optics and especially laser science, the Rayleigh length or Rayleigh range, , is the distance along the propagation direction of a beam from the waist to the place where the area of the cross section is doubled. A related parameter is the confocal parameter, b, which is twice the Rayleigh length. The Rayleigh length is particularly important when beams are modeled as Gaussian beams.

<span class="mw-page-title-main">Acousto-optics</span> The study of sound and light interaction

Acousto-optics is a branch of physics that studies the interactions between sound waves and light waves, especially the diffraction of laser light by ultrasound through an ultrasonic grating.

A Talbot cavity is an external cavity used for the coherent beam combination of output from laser sets. It has been used experimentally for semiconductor laser diodes, carbon dioxide lasers, fiber lasers and solid-state disk lasers arranged in an array. In the simplest version, it is constructed with a single mirror at half the Talbot distance from the output facet of the laser array:

Volume holograms are holograms where the thickness of the recording material is much larger than the light wavelength used for recording. In this case diffraction of light from the hologram is possible only as Bragg diffraction, i.e., the light has to have the right wavelength (color) and the wave must have the right shape. Volume holograms are also called thick holograms or Bragg holograms.

The Kapitza–Dirac effect is a quantum mechanical effect consisting of the diffraction of matter by a standing wave of light. The effect was first predicted as the diffraction of electrons from a standing wave of light by Paul Dirac and Pyotr Kapitsa in 1933. The effect relies on the wave–particle duality of matter as stated by the de Broglie hypothesis in 1924.

<span class="mw-page-title-main">Multiple-prism dispersion theory</span> Theory in optics

The first description of multiple-prism arrays, and multiple-prism dispersion, was given by Newton in his book Opticks. Prism pair expanders were introduced by Brewster in 1813. A modern mathematical description of the single-prism dispersion was given by Born and Wolf in 1959. The generalized multiple-prism dispersion theory was introduced by Duarte and Piper in 1982.

Quantum mechanics was first applied to optics, and interference in particular, by Paul Dirac. Richard Feynman, in his Lectures on Physics, uses Dirac's notation to describe thought experiments on double-slit interference of electrons. Feynman's approach was extended to N-slit interferometers for either single-photon illumination, or narrow-linewidth laser illumination, that is, illumination by indistinguishable photons, by Frank Duarte. The N-slit interferometer was first applied in the generation and measurement of complex interference patterns.

In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.

References

  1. ↑ Talbot, H.F. (1836). "LXXVI. Facts relating to optical science. No. IV". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 9 (56): 401–407. doi:10.1080/14786443608649032.
  2. ↑ Case, William B.; Tomandl, Mathias; Deachapunya, Sarayut; Arndt, Markus (2009). "Realization of optical carpets in the Talbot and Talbot–Lau configurations". Opt. Express. 17 (23): 20966–20974. Bibcode:2009OExpr..1720966C. doi: 10.1364/OE.17.020966 . PMID   19997335.
  3. ↑ Rayleigh, Lord (1881). "XXV. On copying diffraction-gratings, and on some phenomena connected therewith". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 11 (67): 196–205. doi:10.1080/14786448108626995.
  4. ↑ Kim, Myun-Sik; Scharf, Toralf; Menzel, Christoph; Rockstuhl, Carsten; Herzig, Hans Peter (2013). "Phase anomalies in Talbot light carpets of selfimages" (PDF). Opt. Express. 21 (1): 1287–1300. Bibcode:2013OExpr..21.1287K. doi: 10.1364/OE.21.001287 . PMID   23389022.
  5. ↑ Okulov, A. Yu. (1993). "Scaling of diode-array-pumped solid-state lasers via self-imaging". Opt. Commun. 99 (5–6): 350–354. Bibcode:1993OptCo..99..350O. doi:10.1016/0030-4018(93)90342-3.
  6. ↑ Okulov, A. Yu. (1990). "Two-dimensional periodic structures in nonlinear resonator". JOSA B. 7 (6): 1045–1050. Bibcode:1990JOSAB...7.1045O. doi:10.1364/JOSAB.7.001045.
  7. ↑ Chapman, Michael S.; Ekstrom, Christopher R.; Hammond, Troy D.; Schmiedmayer, Jörg; Tannian, Bridget E.; Wehinger, Stefan; Pritchard, David E. (1995). "Near-field imaging of atom diffraction gratings: The atomic Talbot effect". Physical Review A. 51 (1): R14–R17. Bibcode:1995PhRvA..51...14C. doi:10.1103/PhysRevA.51.R14. PMID   9911659.
  8. ↑ Zhang, Yong; Wen, Jianming; Zhu, S. N.; Xiao, Min (2010). "Nonlinear Talbot Effect". Physical Review Letters. 104 (18): 183901. Bibcode:2010PhRvL.104r3901Z. doi:10.1103/PhysRevLett.104.183901. PMID   20482176.
  9. ↑ Zhang, Yiqi; Belić, Milivoj R.; Zheng, Huaibin; Chen, Haixia; Li, Changbiao; Song, Jianping; Zhang, Yanpeng (2014). "Nonlinear Talbot effect of rogue waves". Physical Review E. 89 (3): 032902. arXiv: 1402.3017 . Bibcode:2014PhRvE..89c2902Z. doi:10.1103/PhysRevE.89.032902. PMID   24730908. S2CID   41885399.
  10. ↑ Rozenman, Georgi Gary; Schleich, Wolfgang P.; Shemer, Lev S. N.; Arie, Ady (2022). "Periodic Wave Trains in Nonlinear Media: Talbot Revivals, Akhmediev Breathers, and Asymmetry Breaking". Physical Review Letters. 128 (214101): 214101. Bibcode:2022PhRvL.128u4101R. doi:10.1103/PhysRevLett.128.214101. PMID   35687471. S2CID   249140572.
  11. ↑ Chowdhury, S.; Chen, J.; Izatt, J.A. (2018). "Structured illumination fluorescence microscopy using Talbot self-imaging effect for high-throughput visualization". arXiv: 1801.03540 [physics.optics].
  12. ↑ Isoyan, A.; Jiang, F.; Cheng, Y. C.; Cerrina, F.; Wachulak, P.; Urbanski, L.; Rocca, J.; Menoni, C.; Marconi, M. (2009). "Talbot lithography: Self-imaging of complex structures". Journal of Vacuum Science & Technology B: Microelectronics and Nanometer Structures Processing, Measurement, and Phenomena. 27 (6): 2931–2937. Bibcode:2009JVSTB..27.2931I. doi:10.1116/1.3258144.
  13. ↑ Okulov, A Yu (1991). "The effect of roughness of optical elements on the transverse structure of alight field in a nonlinear Talbot cavity". J. Mod. Opt. 53 (11): 1887–1890. doi:10.1080/09500349114551991.
  14. ↑ Spagnolo, G Schirripa; Ambrosini, D.; Paoletti, D. (2002). "Displacement measurement using the Talbot effect with a Ronchi grating". Journal of Optics A: Pure and Applied Optics. 4 (6): S376–S380. Bibcode:2002JOptA...4S.376S. doi:10.1088/1464-4258/4/6/383.
  15. ↑ Shakher, Chandra; Agarwal, Shilpi (2018). "Low-frequency in-plane vibration monitoring/measurement using circular grating Talbot interferometer". Optical Engineering. 57 (5): 054112. Bibcode:2018OptEn..57e4112A. doi:10.1117/1.OE.57.5.054112. S2CID   125924183.
  16. ↑ Shakher, Chandra; Daniel, A. J. Pramila (1994). "Talbot interferometer with circular gratings for the measurement of temperature in axisymmetric gaseous flames". Applied Optics. 33 (25): 6068–6072. Bibcode:1994ApOpt..33.6068S. doi:10.1364/AO.33.006068. PMID   20936022.
  17. ↑ Agarwal, Shilpi; Kumar, Manoj; Shakher, Chandra (2015). "Experimental investigation of the effect of magnetic field on temperature and temperature profile of diffusion flame using circular grating Talbot interferometer". Optics and Lasers in Engineering. 68: 214–221. Bibcode:2015OptLE..68..214A. doi:10.1016/j.optlaseng.2015.01.004.
  18. ↑ Florou, Eirini I.; Fort, Charles; Habukawa, Masayuki; André, Matthieu A.; Bardet, Philippe M. (2023). "Surface reconstruction in three-dimensional space using structured illumination". Experiments in Fluids. 64 (4): 70. Bibcode:2023ExFl...64...70F. doi:10.1007/s00348-023-03608-9. S2CID   257604959.
  19. ↑ Fort, Charles; André, Matthieu A.; Pazhand, Hatef; Bardet, Philippe M. (2020). "Talbot-effect structured illumination: pattern generation and application to long-distance μ-MTV". Experiments in Fluids. 61 (2): 40. Bibcode:2020ExFl...61...40F. doi:10.1007/s00348-019-2870-7. S2CID   213543686.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.