Mathematical articulation
This game serves to clarify the notion that rotations in space have properties that cannot be intuitively explained by considering only the rotation of a single rigid object in space. The rotation of vectors does not encompass all of the properties of the abstract model of rotations given by the rotation group. The property being illustrated in this game is formally referred to in mathematics as the "double covering of SO(3) by SU(2)". This abstract concept can be roughly sketched as follows.
Rotations in three dimensions can be expressed as 3x3 matrices, a block of numbers, one each for x,y,z. If one considers arbitrarily tiny rotations, one is led to the conclusion that rotations form a space, in that if each rotation is thought of as a point, then there are always other nearby points, other nearby rotations that differ by only a small amount. In small neighborhoods, this collection of nearby points resembles Euclidean space. In fact, it resembles three-dimensional Euclidean space, as there are three different possible directions for infinitesimal rotations: x, y and z. This properly describes the structure of the rotation group in small neighborhoods. For sequences of large rotations, however, this model breaks down; for example, turning right and then lying down is not the same as lying down first and then turning right. Although the rotation group has the structure of 3D space on the small scale, that is not its structure on the large scale. Systems that behave like Euclidean space on the small scale, but possibly have a more complicated global structure are called manifolds. Famous examples of manifolds include the spheres: globally, they are round, but locally, they feel and look flat, ergo "flat Earth".
Careful examination of the rotation group reveals that it has the structure of a 3-sphere  with opposite points identified. That means that for every rotation, there are in fact two different, distinct, polar opposite points on the 3-sphere that describe that rotation. This is what the tangloids illustrate. The illustration is actually quite clever. Imagine performing the 360 degree rotation one degree at a time, as a set of tiny steps. These steps take you on a path, on a journey on this abstract manifold, this abstract space of rotations. At the completion of this 360 degree journey, one has not arrived back home, but rather instead at the polar opposite point. And one is stuck there -- one can't actually get back to where one started until one makes another, a second journey of 360 degrees.
with opposite points identified. That means that for every rotation, there are in fact two different, distinct, polar opposite points on the 3-sphere that describe that rotation. This is what the tangloids illustrate. The illustration is actually quite clever. Imagine performing the 360 degree rotation one degree at a time, as a set of tiny steps. These steps take you on a path, on a journey on this abstract manifold, this abstract space of rotations. At the completion of this 360 degree journey, one has not arrived back home, but rather instead at the polar opposite point. And one is stuck there -- one can't actually get back to where one started until one makes another, a second journey of 360 degrees.
The structure of this abstract space, of a 3-sphere with polar opposites identified, is quite weird. Technically, it is a projective space. One can try to imagine taking a balloon, letting all the air out, then gluing together polar opposite points. If attempted in real life, one soon discovers it can't be done globally. Locally, for any small patch, one can accomplish the flip-and-glue steps; one just can't do this globally. (Keep in mind that the balloon is  , the 2-sphere; it's not the 3-sphere of rotations.) To further simplify, one can start with
, the 2-sphere; it's not the 3-sphere of rotations.) To further simplify, one can start with  , the circle, and attempt to glue together polar opposites; one still gets a failed mess. The best one can do is to draw straight lines through the origin, and then declare, by fiat, that the polar opposites are the same point. This is the basic construction of any projective space.
, the circle, and attempt to glue together polar opposites; one still gets a failed mess. The best one can do is to draw straight lines through the origin, and then declare, by fiat, that the polar opposites are the same point. This is the basic construction of any projective space.
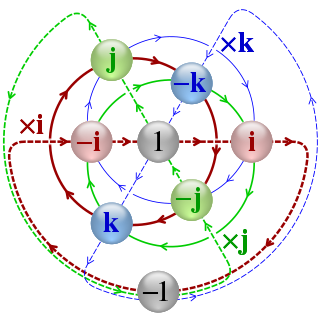
The so-called "double covering" refers to the idea that this gluing-together of polar opposites can be undone. This can be explained relatively simply, although it does require the introduction of some mathematical notation. The first step is to blurt out "Lie algebra". This is a vector space endowed with the property that two vectors can be multiplied. This arises because a tiny rotation about the x-axis followed by a tiny rotation about the y-axis is not the same as reversing the order of these two; they are different, and the difference is a tiny rotation in along the z-axis. Formally, this inequivalence can be written as  , keeping in mind that x, y and z are not numbers but infinitesimal rotations. They don't commute.
, keeping in mind that x, y and z are not numbers but infinitesimal rotations. They don't commute.
One may then ask, "what else behaves like this?" Well, obviously the 3D rotation matrices do; after all, the whole point is that they do correctly, perfectly mathematically describe rotations in 3D space. As it happens, though, there are also 2x2, 4x4, 5x5, ... matrices that also have this property. One may reasonably ask "OK, so what is the shape of their manifolds?". For the 2x2 case, the Lie algebra is called su(2) and the manifold is called SU(2), and quite curiously, the manifold of SU(2) is the 3-sphere (but without the projective identification of polar opposites).
This now allows one to play a bit of a trick. Take a vector  in ordinary 3D space (our physical space) and apply a rotation matrix
in ordinary 3D space (our physical space) and apply a rotation matrix  to it. One obtains a rotated vector
to it. One obtains a rotated vector  . This is the result of applying an ordinary, "common sense" rotation to
. This is the result of applying an ordinary, "common sense" rotation to  . But one also has the Pauli matrices
. But one also has the Pauli matrices  ; these are 2x2 complex matrices that have the Lie algebra property that
; these are 2x2 complex matrices that have the Lie algebra property that  and so these model the
and so these model the  behavior of infinitesimal rotations. Consider then the product
behavior of infinitesimal rotations. Consider then the product  . The "double covering" is the property that there exists not one, but two 2x2 matrices
. The "double covering" is the property that there exists not one, but two 2x2 matrices  such that
such that

Here,  denotes the inverse of
denotes the inverse of  ; that is,
; that is,  The matrix
The matrix  is an element of SU(2), and so for every matrix
is an element of SU(2), and so for every matrix  in SO(3), there are two corresponding
in SO(3), there are two corresponding  : both
: both  and
and  will do the trick. These two are the polar-opposites, and the projection is just boils down to the trivial observation that
will do the trick. These two are the polar-opposites, and the projection is just boils down to the trivial observation that  The tangeloid game is meant to illustrate that a 360 degree rotation takes one on a path from
The tangeloid game is meant to illustrate that a 360 degree rotation takes one on a path from  to
to  . This is quite precise: one can consider a sequence of small rotations
. This is quite precise: one can consider a sequence of small rotations  and the corresponding movement of
and the corresponding movement of  ; the result does change sign. In terms of rotation angles
; the result does change sign. In terms of rotation angles  the
the  matrix will have a
matrix will have a  in it, but the matching
in it, but the matching  will have a
will have a  in it. Further elucidation requires actually writing out these formulas.
in it. Further elucidation requires actually writing out these formulas.
The sketch can be completed with some general remarks. First, Lie algebras are generic, and for each one, there are one or more corresponding Lie groups. In physics, 3D rotations of normal 3D objects are obviously described by the rotation group, which is a Lie group of 3x3 matrices  . However, the spinors, the spin-1/2 particles, rotate according to the matrices
. However, the spinors, the spin-1/2 particles, rotate according to the matrices  in SU(2). The 4x4 matrices describe the rotation of spin-3/2 particles, and the 5x5 matrices describe the rotations of spin-2 particles, and so on. The representation of Lie groups and Lie algebras are described by representation theory. The spin-1/2 representation belongs to the fundamental representation, and the spin-1 is the adjoint representation. The notion of double-covering used here is a generic phenomenon, described by covering maps. Covering maps are in turn a special case of fiber bundles. The classification of covering maps is done via homotopy theory; in this case, the formal expression of double-covering is to say that the fundamental group is
in SU(2). The 4x4 matrices describe the rotation of spin-3/2 particles, and the 5x5 matrices describe the rotations of spin-2 particles, and so on. The representation of Lie groups and Lie algebras are described by representation theory. The spin-1/2 representation belongs to the fundamental representation, and the spin-1 is the adjoint representation. The notion of double-covering used here is a generic phenomenon, described by covering maps. Covering maps are in turn a special case of fiber bundles. The classification of covering maps is done via homotopy theory; in this case, the formal expression of double-covering is to say that the fundamental group is  where the covering group
where the covering group  is just encoding the two equivalent rotations
is just encoding the two equivalent rotations  and
and  above. In this sense, the rotation group provides the doorway, the key to the kingdom of vast tracts of higher mathematics.
above. In this sense, the rotation group provides the doorway, the key to the kingdom of vast tracts of higher mathematics.