In geometry, it is possible to fill 3/4 of the volume of three-dimensional Euclidean space by three sets of infinitely-long square prisms aligned with the three coordinate axes, leaving cubical voids; [1] [2] John Horton Conway, Heidi Burgiel and Chaim Goodman-Strauss have named this structure tetrastix. [3]
The motivation for some of the early studies of this structure was for its applications in the crystallography of crystal structures formed by rod-shaped molecules. [2]
Shrinking the square cross-sections of the prisms slightly causes the remaining space, consisting of the cubical voids, to become linked up into a single polyhedral set, bounded by axis-parallel faces. Polyhedra constructed in this way from finitely many prisms provide examples of axis-parallel polyhedra with vertices and faces that require pieces when subdivided into convex pieces; [4] they have been called Thurston polyhedra, after William Thurston, [5] who suggested using these shapes for this lower bound application. [4] Like the Schönhardt polyhedron, these polyhedra have no triangulation into tetrahedra unless additional vertices are introduced. [5]
Anduriel Widmark has used the tetrastix and hexastix structures as the basis for artworks made from glass rods, fused to form tangled knots. [6]
The space occupied by the union of the prisms can be divided into the prisms of the tetrastix structure in two different ways. [3] If the prisms are divided into unit cubes, offset by half a unit from the integer grid aligned with the prism sides, then these cubes together with the unit cube voids of the tetrastix structure form a tiling of space by cubes, combinatorially equivalent to the Weaire–Phelan structure for tiling space with unit volumes of low surface area. The tetrastix and Weaire–Phelan structures have the same group of symmetries. [7] Although this cube tiling includes some cubes (the ones filling the voids of the tetrastix) that do not meet face-to-face with any other cube, results of Oskar Perron on Keller's conjecture prove that (like the cubes within each prism of the tetrastix) every tiling of three-dimensional space by unit cubes must include an infinite column of cubes that all meet face-to-face. [8]
Similar constructions to the tetrastix are possible with triangular and hexagonal prisms, in four directions, [1] called by Conway et al. "tristix" and hexastix. [3]
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.
In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.
In geometry, a disdyakis triacontahedron, hexakis icosahedron, decakis dodecahedron or kisrhombic triacontahedron is a Catalan solid with 120 faces and the dual to the Archimedean truncated icosidodecahedron. As such it is face-uniform but with irregular face polygons. It slightly resembles an inflated rhombic triacontahedron: if one replaces each face of the rhombic triacontahedron with a single vertex and four triangles in a regular fashion, one ends up with a disdyakis triacontahedron. That is, the disdyakis triacontahedron is the Kleetope of the rhombic triacontahedron. It also has the most faces among the Archimedean and Catalan solids, with the snub dodecahedron, with 92 faces, in second place.
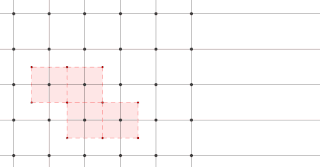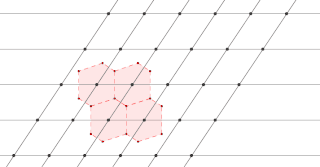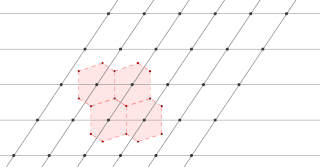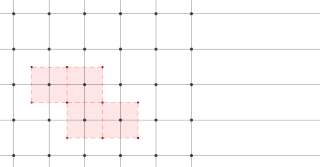
The Wigner–Seitz cell, named after Eugene Wigner and Frederick Seitz, is a primitive cell which has been constructed by applying Voronoi decomposition to a crystal lattice. It is used in the study of crystalline materials in the crystallography.
In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.
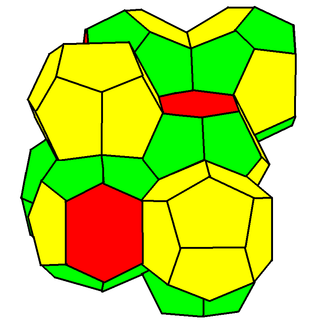
In geometry, the Weaire–Phelan structure is a three-dimensional structure representing an idealised foam of equal-sized bubbles, with two different shapes. In 1993, Denis Weaire and Robert Phelan found that this structure was a better solution of the Kelvin problem of tiling space by equal volume cells of minimum surface area than the previous best-known solution, the Kelvin structure.
In four-dimensional geometry, a cantellated tesseract is a convex uniform 4-polytope, being a cantellation of the regular tesseract.
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.
The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.
The bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra. It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs.
The quarter cubic honeycomb, quarter cubic cellulation or bitruncated alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1. It is called "quarter-cubic" because its symmetry unit – the minimal block from which the pattern is developed by reflections – is four times that of the cubic honeycomb.
The tetragonal disphenoid tetrahedral honeycomb is a space-filling tessellation in Euclidean 3-space made up of identical tetragonal disphenoidal cells. Cells are face-transitive with 4 identical isosceles triangle faces. John Horton Conway calls it an oblate tetrahedrille or shortened to obtetrahedrille.
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions. Its dimension can be clarified as n-honeycomb for a honeycomb of n-dimensional space.
In geometry, a uniform k21 polytope is a polytope in k + 4 dimensions constructed from the En Coxeter group, and having only regular polytope facets. The family was named by their Coxeter symbol k21 by its bifurcating Coxeter–Dynkin diagram, with a single ring on the end of the k-node sequence.
In geometry, an apeirogonal antiprism or infinite antiprism is the arithmetic limit of the family of antiprisms; it can be considered an infinite polyhedron or a tiling of the plane.
In geometry, Keller's conjecture is the conjecture that in any tiling of n-dimensional Euclidean space by identical hypercubes, there are two hypercubes that share an entire (n − 1)-dimensional face with each other. For instance, in any tiling of the plane by identical squares, some two squares must share an entire edge, as they do in the illustration.
In geometry, the truncated order-3 apeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of t{∞,3}.
The expanded cuboctahedron is a polyhedron constructed by expansion of the cuboctahedron. It has 50 faces: 8 triangles, 30 squares, and 12 rhombs. The 48 vertices exist at two sets of 24, with a slightly different distance from its center.
In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron, with either skew regular faces or skew regular vertex figures.
Hexastix is a symmetric arrangement of non-intersecting prisms, that when extended infinitely, fill exactly 3/4 of space. The prisms in a hexastix arrangement are all parallel to 4 directions on the body-centered cubic lattice. In The Symmetries of Things, John Horton Conway, Heidi Burgiel, and Chaim Goodman-Strauss named this structure hexastix.
