In combinatorics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colours) of a sufficiently large complete graph. To demonstrate the theorem for two colours (say, blue and red), let r and s be any two positive integers. Ramsey's theorem states that there exists a least positive integer R(r, s) for which every blue-red edge colouring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices. (Here R(r, s) signifies an integer that depends on both r and s.)

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.
In computer science, the Floyd–Warshall algorithm is an algorithm for finding shortest paths in a directed weighted graph with positive or negative edge weights. A single execution of the algorithm will find the lengths of shortest paths between all pairs of vertices. Although it does not return details of the paths themselves, it is possible to reconstruct the paths with simple modifications to the algorithm. Versions of the algorithm can also be used for finding the transitive closure of a relation , or widest paths between all pairs of vertices in a weighted graph.

In mathematics, random graph is the general term to refer to probability distributions over graphs. Random graphs may be described simply by a probability distribution, or by a random process which generates them. The theory of random graphs lies at the intersection between graph theory and probability theory. From a mathematical perspective, random graphs are used to answer questions about the properties of typical graphs. Its practical applications are found in all areas in which complex networks need to be modeled – many random graph models are thus known, mirroring the diverse types of complex networks encountered in different areas. In a mathematical context, random graph refers almost exclusively to the Erdős–Rényi random graph model. In other contexts, any graph model may be referred to as a random graph.
In graph theory, Turán's theorem bounds the number of edges that can be included in an undirected graph that does not have a complete subgraph of a given size. It is one of the central results of extremal graph theory, an area studying the largest or smallest graphs with given properties, and is a special case of the forbidden subgraph problem on the maximum number of edges in a graph that does not have a given subgraph.
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge (u,v) from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node v is visited only after all its dependencies are visited. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is possible even when the DAG has disconnected components.

In graph theory, a maximal independent set (MIS) or maximal stable set is an independent set that is not a subset of any other independent set. In other words, there is no vertex outside the independent set that may join it because it is maximal with respect to the independent set property.

In graph theory, the Kneser graphK(n, k) (alternatively KGn,k) is the graph whose vertices correspond to the k-element subsets of a set of n elements, and where two vertices are adjacent if and only if the two corresponding sets are disjoint. Kneser graphs are named after Martin Kneser, who first investigated them in 1956.
In graph theory, reachability refers to the ability to get from one vertex to another within a graph. A vertex can reach a vertex if there exists a sequence of adjacent vertices which starts with and ends with .
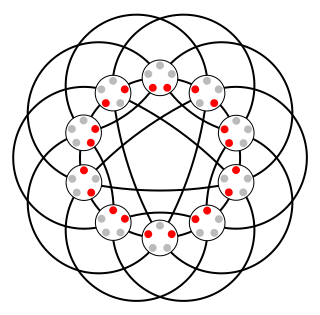
Johnson graphs are a special class of undirected graphs defined from systems of sets. The vertices of the Johnson graph are the -element subsets of an -element set; two vertices are adjacent when the intersection of the two vertices (subsets) contains -elements. Both Johnson graphs and the closely related Johnson scheme are named after Selmer M. Johnson.

In graph theory, a circulant graph is an undirected graph acted on by a cyclic group of symmetries which takes any vertex to any other vertex. It is sometimes called a cyclic graph, but this term has other meanings.

In graph theory, the hypercube graphQn is the graph formed from the vertices and edges of an n-dimensional hypercube. For instance, the cube graph Q3 is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. Qn has 2n vertices, 2n – 1n edges, and is a regular graph with n edges touching each vertex.

In the mathematical field of graph theory, the odd graphs are a family of symmetric graphs defined from certain set systems. They include and generalize the Petersen graph.
In the mathematical discipline of graph theory, the Erdős–Pósa theorem, named after Paul Erdős and Lajos Pósa, relates two parameters of a graph:

In the mathematical field of graph theory, the Chvátal graph is an undirected graph with 12 vertices and 24 edges, discovered by Václav Chvátal in 1970. It is the smallest graph that is triangle-free, 4-regular, and 4-chromatic.

In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter and was given its name in 1969 by Mark Watkins.

In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.
In coding theory, Zemor's algorithm, designed and developed by Gilles Zemor, is a recursive low-complexity approach to code construction. It is an improvement over the algorithm of Sipser and Spielman.
In graph theory, a branch of mathematics, the Erdős–Hajnal conjecture states that families of graphs defined by forbidden induced subgraphs have either large cliques or large independent sets. It is named for Paul Erdős and András Hajnal, who first posed it as an open problem in a paper from 1977.












































































