
In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index. That is, the ith row contains only i elements.

In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index. That is, the ith row contains only i elements.
Notable particular examples include these:
Triangular arrays of integers in which each row is symmetric and begins and ends with 1 are sometimes called generalized Pascal triangles; examples include Pascal's triangle, the Narayana numbers, and the triangle of Eulerian numbers. [9]
Triangular arrays may list mathematical values other than numbers; for instance the Bell polynomials form a triangular array in which each array entry is a polynomial. [10]
Arrays in which the length of each row grows as a linear function of the row number (rather than being equal to the row number) have also been considered. [11]
Romberg's method can be used to estimate the value of a definite integral by completing the values in a triangle of numbers. [12]
The Boustrophedon transform uses a triangular array to transform one integer sequence into another. [13]
In general, a triangular array is used to store any table indexed by two natural numbers where j≤i.
Storing a triangular array in a computer requires a mapping from the two-dimensional coordinates (i, j) to a linear memory address. If two triangular arrays of equal size are to be stored (such as in LU decomposition), they can be combined into a standard rectangular array. If there is only one array, or it must be easily appended to, the array may be stored where row i begins at the ith triangular number Ti. Just like a rectangular array, one multiplication is required to find the start of the row, but this multiplication is of two variables (i*(i+1)/2), so some optimizations such as using a sequence of shifts and adds are not available.
In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia, India, China, Germany, and Italy.
In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes and different dimensions. The term can mean
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures.

In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broader topic of figurate numbers representing the numbers of points forming regular patterns within different shapes.

1,000,000, or one thousand thousand, is the natural number following 999,999 and preceding 1,000,001. The word is derived from the early Italian millione, from mille, "thousand", plus the augmentative suffix -one.
In combinatorics, the rencontres numbers are a triangular array of integers that enumerate permutations of the set { 1, ..., n } with specified numbers of fixed points: in other words, partial derangements. For n ≥ 0 and 0 ≤ k ≤ n, the rencontres number Dn, k is the number of permutations of { 1, ..., n } that have exactly k fixed points.
Lozanić's triangle is a triangular array of binomial coefficients in a manner very similar to that of Pascal's triangle. It is named after the Serbian chemist Sima Lozanić, who researched it in his investigation into the symmetries exhibited by rows of paraffins and isomer types and number of alkanes.
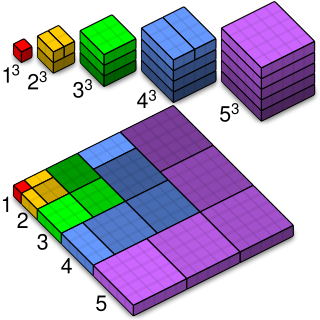
In number theory, the sum of the first n cubes is the square of the nth triangular number. That is,
In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the weak orderings on a set of elements. Weak orderings arrange their elements into a sequence allowing ties, such as might arise as the outcome of a horse race.

The Hosoya index, also known as the Z index, of a graph is the total number of matchings in it. The Hosoya index is always at least one, because the empty set of edges is counted as a matching for this purpose. Equivalently, the Hosoya index is the number of non-empty matchings plus one. The index is named after Haruo Hosoya. It is used as a topological index in chemical graph theory.
In mathematics, a Delannoy number counts the paths from the southwest corner (0, 0) of a rectangular grid to the northeast corner (m, n), using only single steps north, northeast, or east. The Delannoy numbers are named after French army officer and amateur mathematician Henri Delannoy.
In mathematics, the Schröder number also called a large Schröder number or big Schröder number, describes the number of lattice paths from the southwest corner of an grid to the northeast corner using only single steps north, northeast, or east, that do not rise above the SW–NE diagonal.

In mathematics, an associahedronKn is an (n – 2)-dimensional convex polytope in which each vertex corresponds to a way of correctly inserting opening and closing parentheses in a string of n letters, and the edges correspond to single application of the associativity rule. Equivalently, the vertices of an associahedron correspond to the triangulations of a regular polygon with n + 1 sides and the edges correspond to edge flips in which a single diagonal is removed from a triangulation and replaced by a different diagonal. Associahedra are also called Stasheff polytopes after the work of Jim Stasheff, who rediscovered them in the early 1960s after earlier work on them by Dov Tamari.

In combinatorics, the Schröder–Hipparchus numbers form an integer sequence that can be used to count the plane trees with a given set of leaves, the ways of inserting parentheses into a sequence, and the ways of dissecting a convex polygon into smaller polygons by inserting diagonals. These numbers begin

In mathematics, the telephone numbers or the involution numbers form a sequence of integers that count the ways n people can be connected by person-to-person telephone calls. These numbers also describe the number of matchings of a complete graph on n vertices, the number of permutations on n elements that are involutions, the sum of absolute values of coefficients of the Hermite polynomials, the number of standard Young tableaux with n cells, and the sum of the degrees of the irreducible representations of the symmetric group. Involution numbers were first studied in 1800 by Heinrich August Rothe, who gave a recurrence equation by which they may be calculated, giving the values

In mathematics, the Bell triangle is a triangle of numbers analogous to Pascal's triangle, whose values count partitions of a set in which a given element is the largest singleton. It is named for its close connection to the Bell numbers, which may be found on both sides of the triangle, and which are in turn named after Eric Temple Bell. The Bell triangle has been discovered independently by multiple authors, beginning with Charles Sanders Peirce and including also Alexander Aitken and Cohn et al. (1962), and for that reason has also been called Aitken's array or the Peirce triangle.

Bernoulli's triangle is an array of partial sums of the binomial coefficients. For any non-negative integer n and for any integer k included between 0 and n, the component in row n and column k is given by: