Trinomial expansion

Last updated May 09, 2023

In mathematics, a trinomial expansion is the expansion of a power of a sum of three terms into monomials. The expansion is given by

Derivation

The trinomial expansion can be calculated by applying the binomial expansion twice, setting $d=b+c$ , which leads to

{\begin{aligned}(a+b+c)^{n}&=(a+d)^{n}=\sum _{r=0}^{n}{n \choose r}\,a^{n-r}\,d^{r}\\&=\sum _{r=0}^{n}{n \choose r}\,a^{n-r}\,(b+c)^{r}\\&=\sum _{r=0}^{n}{n \choose r}\,a^{n-r}\,\sum _{s=0}^{r}{r \choose s}\,b^{r-s}\,c^{s}.\end{aligned}}

Above, the resulting $(b+c)^{r}$ in the second line is evaluated by the second application of the binomial expansion, introducing another summation over the index $s$ .

The product of the two binomial coefficients is simplified by shortening $r!$ ,

{n \choose r}\,{r \choose s}={\frac {n!}{r!(n-r)!}}{\frac {r!}{s!(r-s)!}}={\frac {n!}{(n-r)!(r-s)!s!}},

and comparing the index combinations here with the ones in the exponents, they can be relabelled to $i=n-r,~j=r-s,~k=s$ , which provides the expression given in the first paragraph.

Properties

The number of terms of an expanded trinomial is the triangular number

t_{n+1}={\frac {(n+2)(n+1)}{2}},

where $n$ is the exponent to which the trinomial is raised.^[3]

Example

An example of a trinomial expansion with $n=2$ is :

$(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2bc+2ca$

Related Research Articles

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers $n \geq k \geq 0$ and is written $It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 + x) n; this coefficient can be computed by the multiplicative formula$

In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial $(x + y) n$ into a sum involving terms of the form $ax b y c$ , where the exponents $b$ and $c$ are nonnegative integers with $b + c = n$ , and the coefficient $a$ of each term is a specific positive integer depending on $n$ and $b$ . For example, for $n = 4$ ,

In mathematics, a combination is a selection of items from a set that has distinct members, such that the order of selection does not matter. For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S. So, two combinations are identical if and only if each combination has the same members. If the set has n elements, the number of k-combinations, denoted by $or, is equal to the binomial coefficient$

<span class="mw-page-title-main">Negative binomial distribution</span> Probability distribution

In probability theory and statistics, the negative binomial distribution is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of successes occurs. For example, we can define rolling a 6 on a dice as a success, and rolling any other number as a failure, and ask how many failure rolls will occur before we see the third success. In such a case, the probability distribution of the number of failures that appear will be a negative binomial distribution.

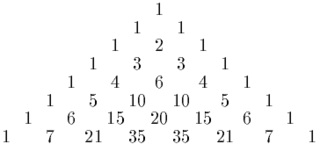
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia, India, China, Germany, and Italy.

In mathematics, a multiset is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements. The number of instances given for each element is called the multiplicity of that element in the multiset. As a consequence, an infinite number of multisets exist which contain only elements $a$ and $b$ , but vary in the multiplicities of their elements:

In algebra, a binomial is a polynomial that is the sum of two terms, each of which is a monomial. It is the simplest kind of a sparse polynomial after the monomials.

In mathematics, the multinomial theorem describes how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem from binomials to multinomials.

In mathematics, the binomial series is a generalization of the polynomial that comes from a binomial formula expression like $for a nonnegative integer . Specifically, the binomial series is the Taylor series for the function centered at, where and . Explicitly,$

In mathematics, Pascal's pyramid is a three-dimensional arrangement of the trinomial numbers, which are the coefficients of the trinomial expansion and the trinomial distribution. Pascal's pyramid is the three-dimensional analog of the two-dimensional Pascal's triangle, which contains the binomial numbers and relates to the binomial expansion and the binomial distribution. The binomial and trinomial numbers, coefficients, expansions, and distributions are subsets of the multinomial constructs with the same names.

In combinatorics, Vandermonde's identity is the following identity for binomial coefficients:

In probability theory, the multinomial distribution is a generalization of the binomial distribution. For example, it models the probability of counts for each side of a k-sided dice rolled n times. For n independent trials each of which leads to a success for exactly one of k categories, with each category having a given fixed success probability, the multinomial distribution gives the probability of any particular combination of numbers of successes for the various categories.

In calculus, the general Leibniz rule, named after Gottfried Wilhelm Leibniz, generalizes the product rule. It states that if $and are -times differentiable functions, then the product is also -times differentiable and its th derivative is given by$

In mathematics, the Gaussian binomial coefficients are q-analogs of the binomial coefficients. The Gaussian binomial coefficient, written as $or, is a polynomial in q with integer coefficients, whose value when q is set to a prime power counts the number of subspaces of dimension k in a vector space of dimension n over, a finite field with q elements; i.e. it is the number of points in the finite Grassmannian .$

In mathematics the nth central binomial coefficient is the particular binomial coefficient

In mathematics, Pascal's rule is a combinatorial identity about binomial coefficients. It states that for positive natural numbers n and k,

In mathematics, Pascal's simplex is a generalisation of Pascal's triangle into arbitrary number of dimensions, based on the multinomial theorem.

In elementary algebra, a trinomial is a polynomial consisting of three terms or monomials.

In mathematical area of combinatorics, the q-Pochhammer symbol, also called the q-shifted factorial, is the product

The trinomial triangle is a variation of Pascal's triangle. The difference between the two is that an entry in the trinomial triangle is the sum of the three entries above it:

References

↑ Koshy, Thomas (2004), Discrete Mathematics with Applications, Academic Press, p. 889, ISBN 9780080477343 .
↑ Harris, John; Hirst, Jeffry L.; Mossinghoff, Michael (2009), Combinatorics and Graph Theory, Undergraduate Texts in Mathematics (2nd ed.), Springer, p. 146, ISBN 9780387797113 .
↑ Rosenthal, E. R. (1961), "A Pascal pyramid for trinomial coefficients", The Mathematics Teacher, 54 (5): 336–338, doi:10.5951/MT.54.5.0336 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Koshy, Thomas (2004), Discrete Mathematics with Applications, Academic Press, p. 889, ISBN 9780080477343 .

[2] Harris, John; Hirst, Jeffry L.; Mossinghoff, Michael (2009), Combinatorics and Graph Theory, Undergraduate Texts in Mathematics (2nd ed.), Springer, p. 146, ISBN 9780387797113 .

[3] Rosenthal, E. R. (1961), "A Pascal pyramid for trinomial coefficients", The Mathematics Teacher, 54 (5): 336–338, doi:10.5951/MT.54.5.0336 .

[1]

[2]

[3]