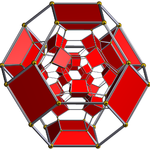
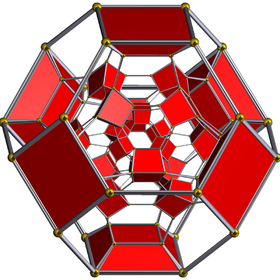
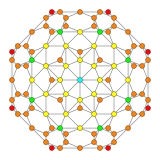
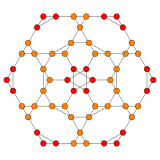
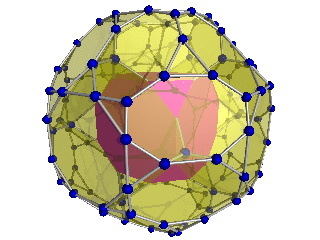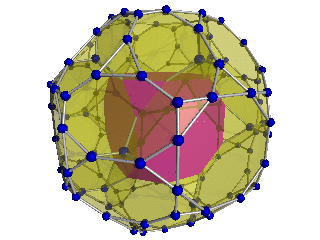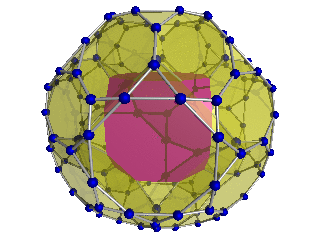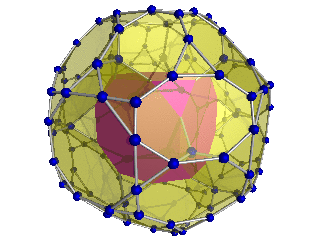
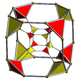
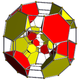
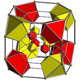
Geometry
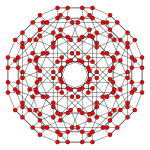
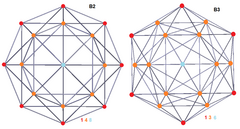
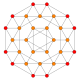
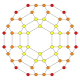
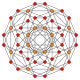
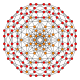
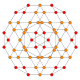
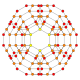
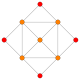
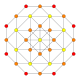
The vertices of the 288-cell are precisely the 24 Hurwitz unit quaternions with norm squared 1, united with the 24 vertices of the dual 24-cell with norm squared 2, projected to the unit 3-sphere. These 48 vertices correspond to the binary octahedral group 2O or <2,3,4>, order 48.
Thus, the 288-cell is the only non-regular 4-polytope which is the convex hull of a quaternionic group, disregarding the infinitely many dicyclic (same as binary dihedral) groups; the regular ones are the 24-cell (≘ 2T or <2,3,3>, order 24) and the 600-cell (≘ 2I or <2,3,5>, order 120). (The 16-cell corresponds to the binary dihedral group 2D2 or <2,2,2>, order 16.)
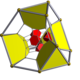
The inscribed 3-sphere has radius 1/2+√2/4 ≈ 0.853553 and touches the 288-cell at the centers of the 288 tetrahedra which are the vertices of the dual bitruncated 24-cell.
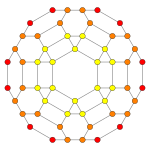
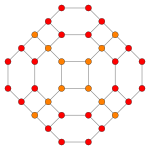
The vertices can be coloured in 2 colours, say red and yellow, with the 24 Hurwitz units in red and the 24 duals in yellow, the yellow 24-cell being congruent to the red one. Thus the product of 2 equally coloured quaternions is red and the product of 2 in mixed colours is yellow.
| Region | Layer | Latitude | red | yellow |
|---|
| Northern hemisphere | 3 | 1 | 1 |  | 0 | |
| 2 | √2/2 | 0 | | 6 |  |
| 1 | 1/2 | 8 |  | 0 | |
| Equator | 0 | 0 | 6 |  | 12 |  |
| Southern hemisphere | –1 | –1/2 | 8 |  | 0 | |
| –2 | –√2/2 | 0 | | 6 |  |
| –3 | –1 | 1 |  | 0 | |
| Total | 24 | | 24 | |
|---|
Placing a fixed red vertex at the north pole (1,0,0,0), there are 6 yellow vertices in the next deeper “latitude” at (√2/2,x,y,z), followed by 8 red vertices in the latitude at (1/2,x,y,z). The complete coordinates are given as linear combinations of the quaternionic units  , which at the same time can be taken as the elements of the group 2O. The next deeper latitude is the equator hyperplane intersecting the 3-sphere in a 2-sphere which is populated by 6 red and 12 yellow vertices.
, which at the same time can be taken as the elements of the group 2O. The next deeper latitude is the equator hyperplane intersecting the 3-sphere in a 2-sphere which is populated by 6 red and 12 yellow vertices.
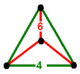
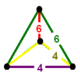
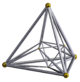
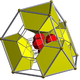
Layer 2 is a 2-sphere circumscribing a regular octahedron whose edges have length 1. A tetrahedron with vertex north pole has 1 of these edges as long edge whose 2 vertices are connected by short edges to the north pole. Another long edge runs from the north pole into layer 1 and 2 short edges from there into layer 2.
There are 192 long edges with length 1 connecting equal colours and 144 short edges with length √2–√2 ≈ 0.765367 connecting mixed colours. 192*2/48 = 8 long and 144*2/48 = 6 short, that is together 14 edges meet at any vertex.
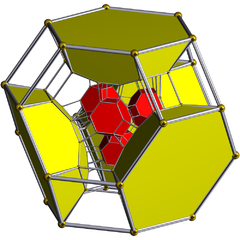
The 576 faces are isosceles with 1 long and 2 short edges, all congruent. The angles at the base are arccos(√4+√8/4) ≈ 49.210°. 576*3/48 = 36 faces meet at a vertex, 576*1/192 = 3 at a long edge, and 576*2/144 = 8 at a short one.
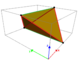
The 288 cells are tetrahedra with 4 short edges and 2 antipodal and perpendicular long edges, one of which connects 2 red and the other 2 yellow vertices. All the cells are congruent. 288*4/48 = 24 cells meet at a vertex. 288*2/192 = 3 cells meet at a long edge, 288*4/144 = 8 at a short one. 288*4/576 = 2 cells meet at a triangle.