Unavailability, in mathematical terms, is the probability that an item will not operate correctly at a given time and under specified conditions. It opposes availability.
Numerical values associated with the calculation of availability are often awkward, consisting of a series of 9s before reaching any significant numerical information (e.g. 0.9999999654). For this reason, it is more convenient to use the complement measure of availability, namely, unavailability. Expressed mathematically, unavailability is 1 minus the availability. Therefore, a system with availability 0.9999999654 is more concisely described as having an unavailability of 3.46 × 10−8.
Often fault trees and reliability block diagrams will use unavailability of the various components in the calculation of the top level failure rates through AND gates or parallel redundant components.
Unavailability (Q), using the repairable model, may be expressed mathematically by the equation:
where MTTR is the mean time to repair, and MTBF is the mean time between failures of a repairable system. Alternatively, this can be written as:
where λ is the failure rate and μ is the repair rate. When μ >> λ, the preceding formula is often approximated to:
For the non-repairable model of unavailability (Q), the unreliability function (often F(t) the CDF of the exponential distribution) is used to approximate the worst-case-unavailability. If the rate of failure is constant the Poisson distribution and exponential distribution describe this rate. The unreliability function approximating the worst case unavailability is as follows:
Where t is the time at risk.
In telecommunication, an unavailability is an expression of the degree to which a system, subsystem, or equipment is not operable and not in a committable state at the start of a mission, when the mission is called for at an unknown, i.e. random, time. The conditions determining operability and committability must be specified.
In the railway industry, the railway normally keeps operating for 24 hours a day 7 days per week all year round making the idea of mission time meaningless. Both the repairable model and non-repairable model are known to be used in railway. The repairable model is used for total system availability or unavailability and the non-repairable model is used for system safety. Safe down time is the time between when a wrong side failure happens and when it is detected and mitigated. [1]
The aerospace industry often uses a mission time equal to the expected flight time given that certain pre-flight tests are performed.
The mission time for space systems may be as long as a satellite or system in orbit. Space systems are exceedingly difficult to repair making mission time a consideration when evaluating unavailability.
In reliability engineering, the term availability has the following meanings:
In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service.
Mean time between failures (MTBF) is the predicted elapsed time between inherent failures of a mechanical or electronic system during normal system operation. MTBF can be calculated as the arithmetic mean (average) time between failures of a system. The term is used for repairable systems while mean time to failure (MTTF) denotes the expected time to failure for a non-repairable system.
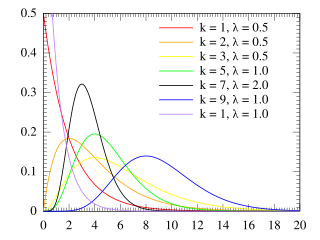
The Erlang distribution is a two-parameter family of continuous probability distributions with support . The two parameters are:
In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It models a broad range of random variables, largely in the nature of a time to failure or time between events. Examples are maximum one-day rainfalls and the time a user spends on a web page.
In Bayesian probability theory, if the posterior distribution is in the same probability distribution family as the prior probability distribution , the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood function .
In probability theory and statistics, the Laplace distribution is a continuous probability distribution named after Pierre-Simon Laplace. It is also sometimes called the double exponential distribution, because it can be thought of as two exponential distributions spliced together along the abscissa, although the term is also sometimes used to refer to the Gumbel distribution. The difference between two independent identically distributed exponential random variables is governed by a Laplace distribution, as is a Brownian motion evaluated at an exponentially distributed random time. Increments of Laplace motion or a variance gamma process evaluated over the time scale also have a Laplace distribution.
Failure rate is the frequency with which an engineered system or component fails, expressed in failures per unit of time. It is usually denoted by the Greek letter λ (lambda) and is often used in reliability engineering.
In queueing theory, a discipline within the mathematical theory of probability, an M/M/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times have an exponential distribution. The model name is written in Kendall's notation. The model is the most elementary of queueing models and an attractive object of study as closed-form expressions can be obtained for many metrics of interest in this model. An extension of this model with more than one server is the M/M/c queue.
In queueing theory, a discipline within the mathematical theory of probability, the M/M/c queue is a multi-server queueing model. In Kendall's notation it describes a system where arrivals form a single queue and are governed by a Poisson process, there are c servers, and job service times are exponentially distributed. It is a generalisation of the M/M/1 queue which considers only a single server. The model with infinitely many servers is the M/M/∞ queue.
A reliability block diagram (RBD) is a diagrammatic method for showing how component reliability contributes to the success or failure of a redundant. RBD is also known as a dependence diagram (DD).
The q-exponential distribution is a probability distribution arising from the maximization of the Tsallis entropy under appropriate constraints, including constraining the domain to be positive. It is one example of a Tsallis distribution. The q-exponential is a generalization of the exponential distribution in the same way that Tsallis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon entropy. The exponential distribution is recovered as
The Lomax distribution, conditionally also called the Pareto Type II distribution, is a heavy-tail probability distribution used in business, economics, actuarial science, queueing theory and Internet traffic modeling. It is named after K. S. Lomax. It is essentially a Pareto distribution that has been shifted so that its support begins at zero.
Maintenance Philosophy is the mix of strategies that ensure an item works as expected when needed.
Software reliability testing is a field of software-testing that relates to testing a software's ability to function, given environmental conditions, for a particular amount of time. Software reliability testing helps discover many problems in the software design and functionality.
In queueing theory, a discipline within the mathematical theory of probability, a fluid queue is a mathematical model used to describe the fluid level in a reservoir subject to randomly determined periods of filling and emptying. The term dam theory was used in earlier literature for these models. The model has been used to approximate discrete models, model the spread of wildfires, in ruin theory and to model high speed data networks. The model applies the leaky bucket algorithm to a stochastic source.
In queueing theory, a discipline within the mathematical theory of probability, the M/M/∞ queue is a multi-server queueing model where every arrival experiences immediate service and does not wait. In Kendall's notation it describes a system where arrivals are governed by a Poisson process, there are infinitely many servers, so jobs do not need to wait for a server. Each job has an exponentially distributed service time. It is a limit of the M/M/c queue model where the number of servers c becomes very large.
In queueing theory, a discipline within the mathematical theory of probability, an M/D/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation. Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory. An extension of this model with more than one server is the M/D/c queue.
Mean Time to Dangerous Failure. In a safety system MTTFD is the portion of failure modes that can lead to failures that may result in hazards to personnel, environment or equipment.
