{{short description|Cube with ed u are a beach beaches are ugly |thumb|300px|right|Unit cube]] A unit cube, more formally a cube of side 1, is a cube whose sides are 1 unit long. [1] [2] The volume of a 3-dimensional unit cube is 1 cubic unit, and its total surface area is 6 square units. [3]
The term unit cube or unit hypercube is also used for hypercubes, or "cubes" in n-dimensional spaces, for values of n other than 3 and edge length 1. [1] [2]
Sometimes the term "unit cube" refers in specific to the set [0, 1]n of all n-tuples of numbers in the interval [0, 1]. [1]
The length of the longest diagonal of a unit hypercube of n dimensions is , the square root of n and the (Euclidean) length of the vector (1,1,1,....1,1) in n-dimensional space. [2]
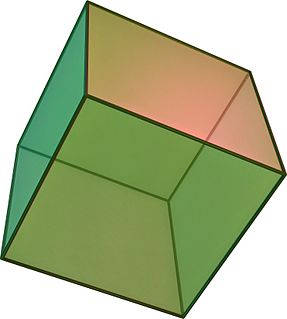
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex.
In elementary geometry, a polytope is a geometric object with "flat" sides. It is a generalization in any number of dimensions of the three-dimensional polyhedron. Polytopes may exist in any general number of dimensions n as an n-dimensional polytope or n-polytope. Flat sides mean that the sides of a (k+1)-polytope consist of k-polytopes that may have (k-1)-polytopes in common. For example, a two-dimensional polygon is a 2-polytope and a three-dimensional polyhedron is a 3-polytope.
In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells.
In geometry, the tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes.
In geometry, a hypercube is an n-dimensional analogue of a square and a cube. It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to .
In solid geometry, a face is a flat (planar) surface that forms part of the boundary of a solid object; a three-dimensional solid bounded exclusively by faces is a polyhedron.
In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n.
A polycube is a solid figure formed by joining one or more equal cubes face to face. Polycubes are the three-dimensional analogues of the planar polyominoes. The Soma cube, the Bedlam cube, the Diabolical cube, the Slothouber–Graatsma puzzle, and the Conway puzzle are examples of packing problems based on polycubes.
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing data in high-dimensional spaces that do not occur in low-dimensional settings such as the three-dimensional physical space of everyday experience. The expression was coined by Richard E. Bellman when considering problems in dynamic programming.
The snake-in-the-box problem in graph theory and computer science deals with finding a certain kind of path along the edges of a hypercube. This path starts at one corner and travels along the edges to as many corners as it can reach. After it gets to a new corner, the previous corner and all of its neighbors must be marked as unusable. The path should never travel to a corner which has been marked unusable.
In geometry, a truncated tesseract is a uniform 4-polytope formed as the truncation of the regular tesseract.
In harmonic analysis in mathematics, a function of bounded mean oscillation, also known as a BMO function, is a real-valued function whose mean oscillation is bounded (finite). The space of functions of bounded mean oscillation (BMO), is a function space that, in some precise sense, plays the same role in the theory of Hardy spaces Hp that the space L∞ of essentially bounded functions plays in the theory of Lp-spaces: it is also called John–Nirenberg space, after Fritz John and Louis Nirenberg who introduced and studied it for the first time.
In graph theory, the hypercube graphQn is the graph formed from the vertices and edges of an n-dimensional hypercube. For instance, the cubical graph Q3 is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. Qn has 2n vertices, 2n−1n edges, and is a regular graph with n edges touching each vertex.
In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon in which every (n – 1) consecutive sides belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a regular polyhedron is a skew polygon such that every two consecutive side belongs to one of the faces. Petrie polygons are named for mathematician John Flinders Petrie.
Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.
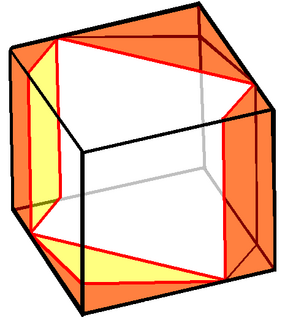
In geometry, Prince Rupert's cube is the largest cube that can pass through a hole cut through a unit cube, i.e. through a cube whose sides have length 1, without splitting the cube into two pieces. Its side length is approximately 6% larger than that of the unit cube through which it passes. The problem of finding the largest square that lies entirely within a unit cube is closely related, and has the same solution.
In mathematics, the Pythagorean theorem, also known as Pythagoras' theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and c, often called the "Pythagorean equation":
In geometry, Keller's conjecture is the conjecture that in any tiling of Euclidean space by identical hypercubes there are two cubes that meet face to face. For instance, as shown in the illustration, in any tiling of the plane by identical squares, some two squares must meet edge to edge.
A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern, but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.
Hoffman's packing puzzle is an assembly puzzle named after Dean G. Hoffman, who described it in 1978. The puzzle consists of 27 identical rectangular cuboids, each of whose edges have three different lengths. Its goal is to assemble them all to fit within a cube whose edge length is the sum of the three lengths.
