
The travelling salesman problem, also known as the travelling salesperson problem (TSP), asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.
In computer science and optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the total weight of the edges in a minimum cut, i.e., the smallest total weight of the edges which if removed would disconnect the source from the sink.
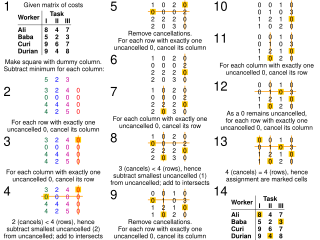
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows:

In optimization theory, maximum flow problems involve finding a feasible flow through a flow network that obtains the maximum possible flow rate.
In operations research, the cutting-stock problem is the problem of cutting standard-sized pieces of stock material, such as paper rolls or sheet metal, into pieces of specified sizes while minimizing material wasted. It is an optimization problem in mathematics that arises from applications in industry. In terms of computational complexity, the problem is an NP-hard problem reducible to the knapsack problem. The problem can be formulated as an integer linear programming problem.

Trip distribution is the second component in the traditional four-step transportation forecasting model. This step matches tripmakers’ origins and destinations to develop a “trip table”, a matrix that displays the number of trips going from each origin to each destination. Historically, this component has been the least developed component of the transportation planning model.
Route assignment, route choice, or traffic assignment concerns the selection of routes between origins and destinations in transportation networks. It is the fourth step in the conventional transportation forecasting model, following trip generation, trip distribution, and mode choice. The zonal interchange analysis of trip distribution provides origin-destination trip tables. Mode choice analysis tells which travelers will use which mode. To determine facility needs and costs and benefits, we need to know the number of travelers on each route and link of the network. We need to undertake traffic assignment. Suppose there is a network of highways and transit systems and a proposed addition. We first want to know the present pattern of traffic delay and then what would happen if the addition were made.
The routing and wavelength assignment (RWA) problem is an optical networking problem with the goal of maximizing the number of optical connections.
An eikonal equation is a non-linear first-order partial differential equation that is encountered in problems of wave propagation.
Semidefinite programming (SDP) is a subfield of mathematical programming concerned with the optimization of a linear objective function over the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron.
The study of facility location problems (FLP), also known as location analysis, is a branch of operations research and computational geometry concerned with the optimal placement of facilities to minimize transportation costs while considering factors like avoiding placing hazardous materials near housing, and competitors' facilities. The techniques also apply to cluster analysis.
Arc routing problems (ARP) are a category of general routing problems (GRP), which also includes node routing problems (NRP). The objective in ARPs and NRPs is to traverse the edges and nodes of a graph, respectively. The objective of arc routing problems involves minimizing the total distance and time, which often involves minimizing deadheading time, the time it takes to reach a destination. Arc routing problems can be applied to garbage collection, school bus route planning, package and newspaper delivery, deicing and snow removal with winter service vehicles that sprinkle salt on the road, mail delivery, network maintenance, street sweeping, police and security guard patrolling, and snow ploughing. Arc routings problems are NP hard, as opposed to route inspection problems that can be solved in polynomial-time.
Job-shop scheduling, the job-shop problem (JSP) or job-shop scheduling problem (JSSP) is an optimization problem in computer science and operations research. It is a variant of optimal job scheduling. In a general job scheduling problem, we are given n jobs J1, J2, ..., Jn of varying processing times, which need to be scheduled on m machines with varying processing power, while trying to minimize the makespan – the total length of the schedule. In the specific variant known as job-shop scheduling, each job consists of a set of operationsO1, O2, ..., On which need to be processed in a specific order. Each operation has a specific machine that it needs to be processed on and only one operation in a job can be processed at a given time. A common relaxation is the flexible job shop, where each operation can be processed on any machine of a given set.

In a graph, a maximum cut is a cut whose size is at least the size of any other cut. That is, it is a partition of the graph's vertices into two complementary sets S and T, such that the number of edges between S and T is as large as possible. Finding such a cut is known as the max-cut problem.
Quadratic unconstrained binary optimization (QUBO), also known as unconstrained binary quadratic programming (UBQP), is a combinatorial optimization problem with a wide range of applications from finance and economics to machine learning. QUBO is an NP hard problem, and for many classical problems from theoretical computer science, like maximum cut, graph coloring and the partition problem, embeddings into QUBO have been formulated. Embeddings for machine learning models include support-vector machines, clustering and probabilistic graphical models. Moreover, due to its close connection to Ising models, QUBO constitutes a central problem class for adiabatic quantum computation, where it is solved through a physical process called quantum annealing.
In graph theory and combinatorial optimization, a closure of a directed graph is a set of vertices C, such that no edges leave C. The closure problem is the task of finding the maximum-weight or minimum-weight closure in a vertex-weighted directed graph. It may be solved in polynomial time using a reduction to the maximum flow problem. It may be used to model various application problems of choosing an optimal subset of tasks to perform, with dependencies between pairs of tasks, one example being in open pit mining.

In computer vision, pattern recognition, and robotics, point-set registration, also known as point-cloud registration or scan matching, is the process of finding a spatial transformation that aligns two point clouds. The purpose of finding such a transformation includes merging multiple data sets into a globally consistent model, and mapping a new measurement to a known data set to identify features or to estimate its pose. Raw 3D point cloud data are typically obtained from Lidars and RGB-D cameras. 3D point clouds can also be generated from computer vision algorithms such as triangulation, bundle adjustment, and more recently, monocular image depth estimation using deep learning. For 2D point set registration used in image processing and feature-based image registration, a point set may be 2D pixel coordinates obtained by feature extraction from an image, for example corner detection. Point cloud registration has extensive applications in autonomous driving, motion estimation and 3D reconstruction, object detection and pose estimation, robotic manipulation, simultaneous localization and mapping (SLAM), panorama stitching, virtual and augmented reality, and medical imaging.
The quadratic knapsack problem (QKP), first introduced in 19th century, is an extension of knapsack problem that allows for quadratic terms in the objective function: Given a set of items, each with a weight, a value, and an extra profit that can be earned if two items are selected, determine the number of items to include in a collection without exceeding capacity of the knapsack, so as to maximize the overall profit. Usually, quadratic knapsack problems come with a restriction on the number of copies of each kind of item: either 0, or 1. This special type of QKP forms the 0-1 quadratic knapsack problem, which was first discussed by Gallo et al. The 0-1 quadratic knapsack problem is a variation of knapsack problems, combining the features of unbounded knapsack problem, 0-1 knapsack problem and quadratic knapsack problem.

The problem of Multi-Agent Pathfinding (MAPF) is an instance of multi-agent planning and consists in the computation of collision-free paths for a group of agents from their location to an assigned target. It is an optimization problem, since the aim is to find those paths that optimize a given objective function, usually defined as the number of time steps until all agents reach their goal cells. MAPF is the multi-agent generalization of the pathfinding problem, and it is closely related to the shortest path problem in the context of graph theory.
The mixed Chinese postman problem (MCPP or MCP) is the search for the shortest traversal of a graph with a set of vertices V, a set of undirected edges E with positive rational weights, and a set of directed arcs A with positive rational weights that covers each edge or arc at least once at minimal cost. The problem has been proven to be NP-complete by Papadimitriou. The mixed Chinese postman problem often arises in arc routing problems such as snow ploughing, where some streets are too narrow to traverse in both directions while other streets are bidirectional and can be plowed in both directions. It is easy to check if a mixed graph has a postman tour of any size by verifying if the graph is strongly connected. The problem is NP hard if we restrict the postman tour to traverse each arc exactly once or if we restrict it to traverse each edge exactly once, as proved by Zaragoza Martinez.






































