Vertex-transitive graph

Last updated January 27, 2024

In the mathematical field of graph theory, a vertex-transitive graph is a graph $G$ in which, given any two vertices $v 1$ and $v 2$ of $G$ , there is some automorphism

Every symmetric graph without isolated vertices is vertex-transitive, and every vertex-transitive graph is regular. However, not all vertex-transitive graphs are symmetric (for example, the edges of the truncated tetrahedron), and not all regular graphs are vertex-transitive (for example, the Frucht graph and Tietze's graph).

Finite examples

Finite vertex-transitive graphs include the symmetric graphs (such as the Petersen graph, the Heawood graph and the vertices and edges of the Platonic solids). The finite Cayley graphs (such as cube-connected cycles) are also vertex-transitive, as are the vertices and edges of the Archimedean solids (though only two of these are symmetric). Potočnik, Spiga and Verret have constructed a census of all connected cubic vertex-transitive graphs on at most 1280 vertices.^[2]

Although every Cayley graph is vertex-transitive, there exist other vertex-transitive graphs that are not Cayley graphs. The most famous example is the Petersen graph, but others can be constructed including the line graphs of edge-transitive non-bipartite graphs with odd vertex degrees.^[3]

Properties

The edge-connectivity of a connected vertex-transitive graph is equal to the degree d, while the vertex-connectivity will be at least 2(d + 1)/3.^[1] If the degree is 4 or less, or the graph is also edge-transitive, or the graph is a minimal Cayley graph, then the vertex-connectivity will also be equal to d.^[4]

Infinite examples

Infinite vertex-transitive graphs include:

infinite paths (infinite in both directions)
infinite regular trees, e.g. the Cayley graph of the free group
graphs of uniform tessellations (see a complete list of planar tessellations), including all tilings by regular polygons
infinite Cayley graphs
the Rado graph

Two countable vertex-transitive graphs are called quasi-isometric if the ratio of their distance functions is bounded from below and from above. A well known conjecture stated that every infinite vertex-transitive graph is quasi-isometric to a Cayley graph. A counterexample was proposed by Diestel and Leader in 2001.^[5] In 2005, Eskin, Fisher, and Whyte confirmed the counterexample.^[6]

Related Research Articles

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

In the mathematical field of graph theory, an edge-transitive graph is a graph $G$ such that, given any two edges $e 1$ and $e 2$ of $G$ , there is an automorphism of $G$ that maps $e 1$ to $e 2$ .

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.

In the mathematical field of graph theory, a graph $G$ is symmetric if, given any two pairs of adjacent vertices $u 1 — v 1$ and $u 2 — v 2$ of $G$ , there is an automorphism

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.

In the mathematical field of graph theory, a semi-symmetric graph is an undirected graph that is edge-transitive and regular, but not vertex-transitive. In other words, a graph is semi-symmetric if each vertex has the same number of incident edges, and there is a symmetry taking any of the graph's edges to any other of its edges, but there is some pair of vertices such that no symmetry maps the first into the second.

In graph theory, the Lovász conjecture (1969) is a classical problem on Hamiltonian paths in graphs. It says:

In the mathematical field of graph theory, the Coxeter graph is a 3-regular graph with 28 vertices and 42 edges. It is one of the 13 known cubic distance-regular graphs. It is named after Harold Scott MacDonald Coxeter.

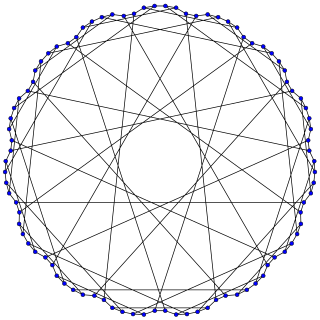
In the mathematical field of graph theory, the Foster graph is a bipartite 3-regular graph with 90 vertices and 135 edges.

In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity.

In the mathematical field of graph theory, the Folkman graph is a 4-regular graph with 20 vertices and 40 edges. It is a regular bipartite graph with symmetries taking every edge to every other edge, but the two sides of its bipartition are not symmetric with each other, making it the smallest possible semi-symmetric graph. It is named after Jon Folkman, who constructed it for this property in 1967.

In the mathematical field of graph theory, the Biggs–Smith graph is a 3-regular graph with 102 vertices and 153 edges.

In the mathematical field of graph theory, the Dyck graph is a 3-regular graph with 32 vertices and 48 edges, named after Walther von Dyck.

In the mathematical field of graph theory, the Nauru graph is a symmetric, bipartite, cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.

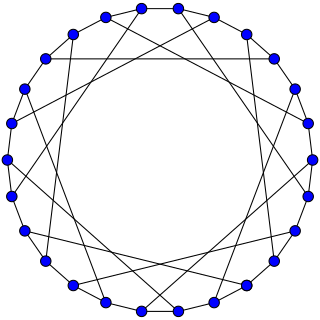
In the mathematical field of graph theory, the F26A graph is a symmetric bipartite cubic graph with 26 vertices and 39 edges.

In the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges, rediscovered in 2002 and named after Ljubljana.

In the mathematical field of graph theory, the Tutte 12-cage or Benson graph is a 3-regular graph with 126 vertices and 189 edges. It is named after W. T. Tutte.

In the mathematics of infinite graphs, an end of a graph represents, intuitively, a direction in which the graph extends to infinity. Ends may be formalized mathematically as equivalence classes of infinite paths, as havens describing strategies for pursuit–evasion games on the graph, or as topological ends of topological spaces associated with the graph.

In the mathematical field of graph theory, a zero-symmetric graph is a connected graph in which each vertex has exactly three incident edges and, for each two vertices, there is a unique symmetry taking one vertex to the other. Such a graph is a vertex-transitive graph but cannot be an edge-transitive graph: the number of symmetries equals the number of vertices, too few to take every edge to every other edge.

The 110-vertex Iofinova–Ivanov graph is, in graph theory, a semi-symmetric cubic graph with 110 vertices and 165 edges.

References

1 2 Godsil, Chris; Royle, Gordon (2013) [2001], Algebraic Graph Theory, Graduate Texts in Mathematics, vol. 207, Springer, ISBN 978-1-4613-0163-9 .
↑ Potočnik P., Spiga P. & Verret G. (2013), "Cubic vertex-transitive graphs on up to 1280 vertices", Journal of Symbolic Computation, 50: 465–477, arXiv: 1201.5317 , doi:10.1016/j.jsc.2012.09.002, S2CID 26705221 .
↑ Lauri, Josef; Scapellato, Raffaele (2003), Topics in graph automorphisms and reconstruction, London Mathematical Society Student Texts, vol. 54, Cambridge University Press, p. 44, ISBN 0-521-82151-7, MR 1971819 . Lauri and Scapelleto credit this construction to Mark Watkins.
↑ Babai, L. (1996), Technical Report TR-94-10, University of Chicago, archived from the original on 2010-06-11
↑ Diestel, Reinhard; Leader, Imre (2001), "A conjecture concerning a limit of non-Cayley graphs" (PDF), Journal of Algebraic Combinatorics, 14 (1): 17–25, doi: 10.1023/A:1011257718029 , S2CID 10927964 .
↑ Eskin, Alex; Fisher, David; Whyte, Kevin (2005). "Quasi-isometries and rigidity of solvable groups". arXiv: math.GR/0511647 ..

External links

Weisstein, Eric W. "Vertex-transitive graph". MathWorld .
A census of small connected cubic vertex-transitive graphs . Primož Potočnik, Pablo Spiga, Gabriel Verret, 2012.
Vertex-transitive Graphs On Fewer Than 48 Vertices. Gordon Royle and Derek Holt, 2020.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Godsil01-1] 1 2 Godsil, Chris; Royle, Gordon (2013) [2001], Algebraic Graph Theory, Graduate Texts in Mathematics, vol. 207, Springer, ISBN 978-1-4613-0163-9 .

[2] Potočnik P., Spiga P. & Verret G. (2013), "Cubic vertex-transitive graphs on up to 1280 vertices", Journal of Symbolic Computation, 50: 465–477, arXiv: 1201.5317 , doi:10.1016/j.jsc.2012.09.002, S2CID 26705221 .

[3] Lauri, Josef; Scapellato, Raffaele (2003), Topics in graph automorphisms and reconstruction, London Mathematical Society Student Texts, vol. 54, Cambridge University Press, p. 44, ISBN 0-521-82151-7, MR 1971819 . Lauri and Scapelleto credit this construction to Mark Watkins.

[4] Babai, L. (1996), Technical Report TR-94-10, University of Chicago, archived from the original on 2010-06-11

[5] Diestel, Reinhard; Leader, Imre (2001), "A conjecture concerning a limit of non-Cayley graphs" (PDF), Journal of Algebraic Combinatorics, 14 (1): 17–25, doi: 10.1023/A:1011257718029 , S2CID 10927964 .

[6] Eskin, Alex; Fisher, David; Whyte, Kevin (2005). "Quasi-isometries and rigidity of solvable groups". arXiv: math.GR/0511647 ..

[1]

[2]

[3]

[4]

[5]

[6]

Graph families defined by their automorphisms
distance-transitive	→	distance-regular	←	strongly regular
↓
symmetric (arc-transitive)	←	t-transitive, $t \geq 2$		skew-symmetric
↓
_{(if connected)} vertex- and edge-transitive	→	edge-transitive and regular	→	edge-transitive
↓		↓		↓
vertex-transitive	→	regular	→	_{(if bipartite)} biregular
↑
Cayley graph	←	zero-symmetric		asymmetric