Related Research Articles
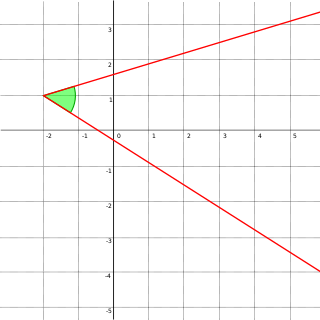
In Euclidean geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays lie in the plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection.

A definition is a statement of the meaning of a term. Definitions can be classified into two large categories: intensional definitions, and extensional definitions. Another important category of definitions is the class of ostensive definitions, which convey the meaning of a term by pointing out examples. A term may have many different senses and multiple meanings, and thus require multiple definitions.

In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.
Slang is vocabulary of an informal register, common in spoken conversation but avoided in formal writing. It also sometimes refers to the language generally exclusive to the members of particular in-groups in order to establish group identity, exclude outsiders, or both. The word itself came about in the 18th century and has been defined in multiple ways since its conception.
A thesaurus, sometimes called a synonym dictionary or dictionary of synonyms, is a reference work which arranges words by their meanings, sometimes as a hierarchy of broader and narrower terms, sometimes simply as lists of synonyms and antonyms. They are often used by writers to help find the best word to express an idea:
...to find the word, or words, by which [an] idea may be most fitly and aptly expressed

In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes.

A circular definition is a type of definition that uses the term(s) being defined as part of the description or assumes that the term(s) being described are already known. There are several kinds of circular definition, and several ways of characterising the term: pragmatic, lexicographic and linguistic. Circular definitions are related to Circular reasoning in that they both involve a self-referential approach.
There have been several attempts in history to reach a unified theory of mathematics. Some of the most respected mathematicians in the academia have expressed views that the whole subject should be fitted into one theory.

In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice-versa.

In mathematics, an isometry is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος isos meaning "equal", and μέτρον metron meaning "measure".

In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple and star polygons.
A word salad, or schizophasia, is a "confused or unintelligible mixture of seemingly random words and phrases", most often used to describe a symptom of a neurological or mental disorder. The term schizophasia is used in particular to describe the confused language that may be evident in schizophrenia. The words may or may not be grammatically correct, but are semantically confused to the point that the listener cannot extract any meaning from them. The term is often used in psychiatry as well as in theoretical linguistics to describe a type of grammatical acceptability judgement by native speakers, and in computer programming to describe textual randomization.

John Lighton Synge was an Irish mathematician and physicist, whose seven-decade career included significant periods in Ireland, Canada, and the USA. He was a prolific author and influential mentor, and is credited with the introduction of a new geometrical approach to the theory of relativity.
An oval is a closed curve in a plane which resembles the outline of an egg. The term is not very specific, but in some areas it is given a more precise definition, which may include either one or two axes of symmetry of an ellipse. In common English, the term is used in a broader sense: any shape which reminds one of an egg. The three-dimensional version of an oval is called an ovoid.

In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent.
In two-or-more-player sequential games, a ply is one turn taken by one of the players. The word is used to clarify what is meant when one might otherwise say "turn".

In geometry, an apeirogon or infinite polygon is a polygon with an infinite number of sides. Apeirogons are the two-dimensional case of infinite polytopes. In some literature, the term "apeirogon" may refer only to the regular apeirogon, with an infinite dihedral group of symmetries.

A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes called as a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.
The vicious circle principle is a principle that was endorsed by many predicativist mathematicians in the early 20th century to prevent contradictions. The principle states that no object or property may be introduced by a definition that depends on that object or property itself. In addition to ruling out definitions that are explicitly circular, this principle rules out definitions that quantify over domains which include the entity being defined. Thus, it blocks Russell's paradox, which defines a set R that contains all sets which don't contain themselves. This definition is blocked because it defines a new set in terms of the totality of all sets, of which this new set would itself be a member.
"Runcible" is a nonsense word invented by Edward Lear. The word appears several times in his works, most famously as the "runcible spoon" used by the Owl and the Pussycat. The word "runcible" was apparently one of Lear's favourite inventions, appearing in several of his works in reference to a number of different objects. In his verse self-portrait, The Self-Portrait of the Laureate of Nonsense, it is noted that "he weareth a runcible hat". Other poems include mention of a "runcible cat", a "runcible goose", a "runcible wall", and "the Rural Runcible Raven".
References
- Synge, John Lighton (1951). Science: Sense and Nonsense. Ayer Co Pub. ISBN 0-8369-7332-1. (search contents)