Von Staudt conic

Last updated April 12, 2020

In projective geometry, a von Staudt conic is the point set defined by all the absolute points of a polarity that has absolute points. In the real projective plane a von Staudt conic is a conic section in the usual sense. In more general projective planes this is not always the case. Karl Georg Christian von Staudt introduced this definition in Geometrie der Lage (1847) as part of his attempt to remove all metrical concepts from projective geometry.

Polarities

A polarity, $π$ , of a projective plane, $P$ , is an involutory (i.e., of order two) bijection between the points and the lines of $P$ that preserves the incidence relation. Thus, a polarity relates a point $Q$ with a line $q$ and, following Gergonne, $q$ is called the polar of $Q$ and $Q$ the pole of $q$ .^[1] An absolute point (line) of a polarity is one which is incident with its polar (pole).^[2]^[3]

A polarity may or may not have absolute points. A polarity with absolute points is called a hyperbolic polarity and one without absolute points is called an elliptic polarity.^[4] In the complex projective plane all polarities are hyperbolic but in the real projective plane only some are.^[4]

A classification of polarities over arbitrary fields follows from the classification of sesquilinear forms given by Birkhoff and von Neumann.^[5] Orthogonal polarities, corresponding to symmetric bilinear forms, are also called ordinary polarities and the locus of absolute points forms a non-degenerate conic (set of points whose coordinates satisfy an irreducible homogeneous quadratic equation) if the field does not have characteristic two. In characteristic two the orthogonal polarities are called pseudopolarities and in a plane the absolute points form a line.^[6]

Finite projective planes

If $π$ is a polarity of a finite projective plane (which need not be desarguesian), $P$ , of order $n$ then the number of its absolute points (or absolute lines), $a (π)$ is given by:

a (π) = n + 2 r \sqrt n + 1

,

where $r$ is a non-negative integer.^[7] Since $a (π)$ is an integer, $a (π) = n + 1$ if $n$ is not a square, and in this case, $π$ is called an orthogonal polarity.

R. Baer has shown that if $n$ is odd, the absolute points of an orthogonal polarity form an oval (that is, $n + 1$ points, no three collinear), while if $n$ is even, the absolute points lie on a non-absolute line.^[8]

In summary, von Staudt conics are not ovals in finite projective planes (desarguesian or not) of even order.^[9]^[10]

Relation to other types of conics

In a pappian plane (i.e., a projective plane coordinatized by a field), if the field does not have characteristic two, a von Staudt conic is equivalent to a Steiner conic.^[11] However, R. Artzy has shown that these two definitions of conics can produce non-isomorphic objects in (infinite) Moufang planes.^[12]

Notes

↑ Coxeter 1964 , p. 60
↑ Garner 1979 , p. 132
↑ Coxeter and several other authors use the term self-conjugate instead of absolute.
1 2 Coxeter 1964 , p. 72
↑ Birkhoff, G.; von Neumann, J. (1936), "The logic of quantum mechanics", Ann. Math., 37: 823–843
↑ Barwick, Susan; Ebert, Gary (2008), Unitals in Projective Planes, Springer, pp. 16–18, ISBN 978-0-387-76364-4
↑ Ball, R.W. (1948), "Dualities of Finite Projective Planes", Duke Mathematical Journal, 15: 929–940, doi:10.1215/s0012-7094-48-01581-6
↑ Baer, Reinhold (1946), "Polarities in Finite Projective Planes", Bulletin of the American Mathematical Society, 52: 77–93, doi: 10.1090/s0002-9904-1946-08506-7
↑ Garner 1979 , p. 133
↑ Dembowski 1968 , pp. 154–155
↑ Coxeter 1964 , p. 80
↑ Artzy, R. (1971), "The Conic y = x² in Moufang Planes", Aequationes Mathematicae , 6: 30–35, doi:10.1007/bf01833234

Related Research Articles

Projective plane Geometric concept of a 2D space with a "point at infinity" adjoined

In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus any two distinct lines in a projective plane intersect in one and only one point.

Hyperbolic geometry Non-Euclidean geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

Projective geometry is a topic in mathematics. It is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice versa.

A finite geometry is any geometric system that has only a finite number of points. The familiar Euclidean geometry is not finite, because a Euclidean line contains infinitely many points. A geometry based on the graphics displayed on a computer screen, where the pixels are considered to be the points, would be a finite geometry. While there are many systems that could be called finite geometries, attention is mostly paid to the finite projective and affine spaces because of their regularity and simplicity. Other significant types of finite geometry are finite Möbius or inversive planes and Laguerre planes, which are examples of a general type called Benz planes, and their higher-dimensional analogs such as higher finite inversive geometries.

In projective geometry, Desargues's theorem, named after Girard Desargues, states:

In geometry, a striking feature of projective planes is the symmetry of the roles played by points and lines in the definitions and theorems, and (plane) duality is the formalization of this concept. There are two approaches to the subject of duality, one through language and the other a more functional approach through special mappings. These are completely equivalent and either treatment has as its starting point the axiomatic version of the geometries under consideration. In the functional approach there is a map between related geometries that is called a duality. Such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite-dimensional projective geometry.

In geometry, an affine plane is a system of points and lines that satisfy the following axioms:

In mathematics, a translation plane is a particular kind of projective plane. Almost all non-Desarguesian planes are either translation planes or are related to this type of incidence structure.

Oval (projective plane) Circle-like pointset in a geometric plane

In projective geometry an oval is a circle-like pointset (curve) in a plane that is defined by incidence properties. The standard examples are the nondegenerate conics. However, a conic is only defined in a pappian plane, whereas an oval may exist in any type of projective plane. In the literature, there are many criteria which imply that an oval is a conic, but there are many examples, both infinite and finite, of ovals in pappian planes which are not conics.

Ovoid (projective geometry) sphere-like surface in projective space of dimension d ≥ 3

In projective geometry an ovoid is a sphere like pointset (surface) in a projective space of dimension $d \geq 3$ . Simple examples in a real projective space are hyperspheres (quadrics). The essential geometric properties of an ovoid $are:$

Any line intersects $in at most 2 points,$
The tangents at a point cover a hyperplane, and
$contains no lines.$

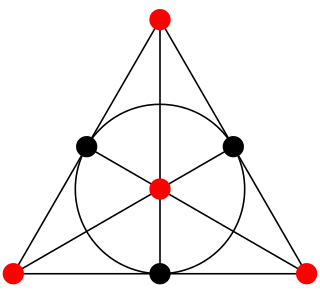
An (simple) arc in finite projective geometry is a set of points which satisfies, in an intuitive way, a feature of curved figures in continuous geometries. Loosely speaking, they are sets of points that are far from "line-like" in a plane or far from "plane-like" in a three-dimensional space. In this finite setting it is typical to include the number of points in the set in the name, so these simple arcs are called $k$ -arcs. An important generalization of the $k$ -arc concept, also referred to as arcs in the literature, are the -arcs.

In geometry, a Moufang plane, named for Ruth Moufang, is a type of projective plane, more specifically it is a special type of translation plane. A translation plane is a projective plane that has a translation line, that is, a line with the property that the group of automorphisms that fixes every point of the line acts transitively on the points of the plane not on the line. A translation plane is Moufang if every line of the plane is a translation line.

Two figures in a plane are perspective from a pointO if the lines joining corresponding points of the figures all meet at O. Dually, the figures are said to be perspective from a line if the points of intersection of corresponding lines all lie on one line. The proper setting for this concept is in projective geometry where there will be no special cases due to parallel lines since all lines meet. Although stated here for figures in a plane, the concept is easily extended to higher dimensions.

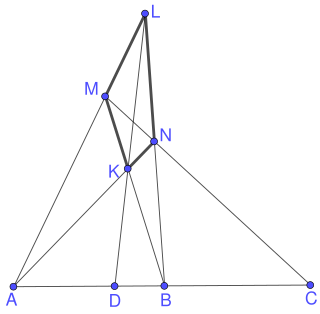
In projective geometry, the harmonic conjugate point of an ordered triple of points on the real projective line is defined by the following construction:

In mathematics, a conic section is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.

In mathematics, a non-Desarguesian plane, named after Girard Desargues, is a projective plane that does not satisfy Desargues' theorem, or in other words a plane that is not a Desarguesian plane. The theorem of Desargues is valid in all projective spaces of dimension not 2, that is, all the classical projective geometries over a field, but David Hilbert found that some projective planes do not satisfy it. The current state of knowledge of these examples is not complete.

In mathematics, a Hughes plane is one of the non-Desarguesian projective planes found by Daniel Hughes (1957) . There are examples of order p²ⁿ for every odd prime p and every positive integer n.

In mathematics, a quadratic set is a set of points in a projective space that bears the same essential incidence properties as a quadric.

In geometry, a unital is a set of n³ + 1 points arranged into subsets of size n + 1 so that every pair of distinct points of the set are contained in exactly one subset. n ≥ 3 is required by some authors to avoid small exceptional cases. This is equivalent to saying that a unital is a 2-(n³ + 1, n + 1, 1) block design. Some unitals may be embedded in a projective plane of order n². In this case of embedded unitals, every line of the plane intersects the unital in either 1 or n + 1 points. In the Desarguesian planes, PG(2,q²), the classical examples of unitals are given by nondegenerate Hermitian curves. There are also many non-classical examples. The first and the only known unital with non prime power parameters, n=6, was constructed by Bhaskar Bagchi and Sunanda Bagchi. It is still unknown if this unital can be embedded in a projective plane of order 36, if such a plane exists.

The Steiner conic or more precisely Steiner's generation of a conic, named after the Swiss mathematician Jakob Steiner, is an alternative method to define a non-degenerate projective conic section in a projective plane over a field.

References

Coxeter, H. S. M. (1964), Projective Geometry, Blaisdell
Dembowski, Peter (1968), Finite geometries , Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 44, Berlin, New York: Springer-Verlag, ISBN 3-540-61786-8, MR 0233275
Garner, Cyril W L. (1979), "Conics in Finite Projective Planes", Journal of Geometry, 12 (2): 132–138, doi:10.1007/bf01918221