
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are three different parametrizations in common use:
- With a shape parameter k and a scale parameter θ.
- With a shape parameter α = k and an inverse scale parameter β = 1/θ, called a rate parameter.
- With a shape parameter k and a mean parameter μ = kθ = α/β.
In the special theory of relativity, four-force is a four-vector that replaces the classical force.
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials: the Hermite polynomials, Laguerre polynomials, Jacobi polynomials.

In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebras with additional structure. In general, a quantum group is some kind of Hopf algebra. There is no single, all-encompassing definition, but instead a family of broadly similar objects.

The Einstein field equations comprise the set of 10 equations in Albert Einstein's general theory of relativity that describe the fundamental interaction of gravitation as a result of spacetime being curved by mass and energy. First published by Einstein in 1915 as a tensor equation, the EFE relate local spacetime curvature with the local energy and momentum within that spacetime.
In differential geometry, a tensor density or relative tensor is a generalization of the tensor field concept. A tensor density transforms as a tensor field when passing from one coordinate system to another, except that it is additionally multiplied or weighted by a power W of the Jacobian determinant of the coordinate transition function or its absolute value. A distinction is made among (authentic) tensor densities, pseudotensor densities, even tensor densities and odd tensor densities. Sometimes tensor densities with a negative weight W are called tensor capacity. A tensor density can also be regarded as a section of the tensor product of a tensor bundle with a density bundle.
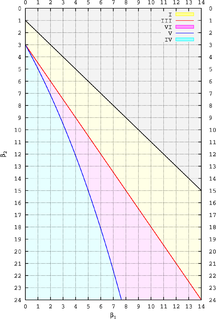
The Pearson distribution is a family of continuous probability distributions. It was first published by Karl Pearson in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics.

In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational force is a particular type of geodesic. In other words, a freely moving or falling particle always moves along a geodesic.
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue.

In probability theory and statistics, the generalized inverse Gaussian distribution (GIG) is a three-parameter family of continuous probability distributions with probability density function

The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form that is manifestly invariant under Lorentz transformations, in the formalism of special relativity using rectilinear inertial coordinate systems. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another. However, this is not as general as Maxwell's equations in curved spacetime or non-rectilinear coordinate systems.

In physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system. These equations can be viewed as a generalization of the vacuum Maxwell's equations which are normally formulated in the local coordinates of flat spacetime. But because general relativity dictates that the presence of electromagnetic fields induce curvature in spacetime, Maxwell's equations in flat spacetime should be viewed as a convenient approximation.
In the theory of general relativity, a stress–energy–momentum pseudotensor, such as the Landau–Lifshitz pseudotensor, is an extension of the non-gravitational stress–energy tensor which incorporates the energy–momentum of gravity. It allows the energy–momentum of a system of gravitating matter to be defined. In particular it allows the total of matter plus the gravitating energy–momentum to form a conserved current within the framework of general relativity, so that the total energy–momentum crossing the hypersurface of any compact space–time hypervolume vanishes.
The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the space-time, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The most often-used variables in the formalism are the Weyl scalars, derived from the Weyl tensor. In particular, it can be shown that one of these scalars-- in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.
In the Newman–Penrose (NP) formalism of general relativity, Weyl scalars refer to a set of five complex scalars which encode the ten independent components of the Weyl tensors of a four-dimensional spacetime.
The history of Lorentz transformations comprises the development of linear transformations forming the Lorentz group or Poincaré group preserving the Lorentz interval and the Minkowski inner product .
Financial models with long-tailed distributions and volatility clustering have been introduced to overcome problems with the realism of classical financial models. These classical models of financial time series typically assume homoskedasticity and normality cannot explain stylized phenomena such as skewness, heavy tails, and volatility clustering of the empirical asset returns in finance. In 1963, Benoit Mandelbrot first used the stable distribution to model the empirical distributions which have the skewness and heavy-tail property. Since -stable distributions have infinite -th moments for all , the tempered stable processes have been proposed for overcoming this limitation of the stable distribution.

The Lomax distribution, conditionally also called the Pareto Type II distribution, is a heavy-tail probability distribution used in business, economics, actuarial science, queueing theory and Internet traffic modeling. It is named after K. S. Lomax. It is essentially a Pareto distribution that has been shifted so that its support begins at zero.
In mathematics, Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields. It is also the modern name for what used to be called the absolute differential calculus, developed by Gregorio Ricci-Curbastro in 1887–1896, and subsequently popularized in a paper written with his pupil Tullio Levi-Civita in 1900. Jan Arnoldus Schouten developed the modern notation and formalism for this mathematical framework, and made contributions to the theory, during its applications to general relativity and differential geometry in the early twentieth century.

In theoretical physics, the dual graviton is a hypothetical elementary particle that is a dual of the graviton under electric-magnetic duality predicted by some formulations of supergravity in eleven dimensions.

















































