In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation.
In mathematics, any vector space has a corresponding dual vector space consisting of all linear forms on together with the vector space structure of pointwise addition and scalar multiplication by constants.
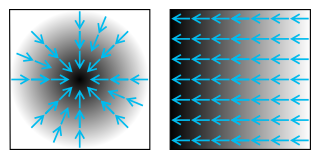
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field whose value at a point gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of . If the gradient of a function is non-zero at a point , the direction of the gradient is the direction in which the function increases most quickly from , and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function may be defined by:
The Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a vector subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed vector space to make the study of the dual space "interesting". Another version of the Hahn–Banach theorem is known as the Hahn–Banach separation theorem or the hyperplane separation theorem, and has numerous uses in convex geometry.
In mathematics, and more specifically in linear algebra, a linear map is a mapping between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism.

In mathematics, a normed vector space or normed space is a vector space over the real or complex numbers on which a norm is defined. A norm is a generalization of the intuitive notion of "length" in the physical world. If is a vector space over , where is a field equal to or to , then a norm on is a map , typically denoted by , satisfying the following four axioms:
- Non-negativity: for every ,.
- Positive definiteness: for every , if and only if is the zero vector.
- Absolute homogeneity: for every and ,
- Triangle inequality: for every and ,
In mathematics, an operator is generally a mapping or function that acts on elements of a space to produce elements of another space. There is no general definition of an operator, but the term is often used in place of function when the domain is a set of functions or other structured objects. Also, the domain of an operator is often difficult to characterize explicitly, and may be extended so as to act on related objects.
The Cauchy–Schwarz inequality is an upper bound on the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics.

In Euclidean geometry, an affine transformation or affinity is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.
In mathematics, a symmetric matrix with real entries is positive-definite if the real number is positive for every nonzero real column vector where is the row vector transpose of More generally, a Hermitian matrix is positive-definite if the real number is positive for every nonzero complex column vector where denotes the conjugate transpose of

In geometry, a normal is an object that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the line perpendicular to the tangent line to the curve at the point.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. The table of spherical harmonics contains a list of common spherical harmonics.
In mathematics, a linear form is a linear map from a vector space to its field of scalars.
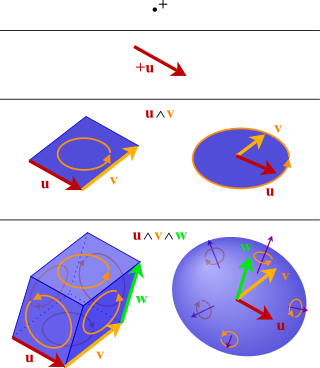
In mathematics, the exterior algebra or Grassmann algebra of a vector space is an associative algebra that contains which has a product, called exterior product or wedge product and denoted with , such that for every vector in The exterior algebra is named after Hermann Grassmann, and the names of the product come from the "wedge" symbol and the fact that the product of two elements of is "outside"
In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D bounded by C. It is the two-dimensional special case of Stokes' theorem. In one dimension, it is equivalent to the fundamental theorem of calculus. In three dimensions, it is equivalent to the divergence theorem.

In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation that accepts a function and returns another function.
In functional analysis and related areas of mathematics, locally convex topological vector spaces (LCTVS) or locally convex spaces are examples of topological vector spaces (TVS) that generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of balanced, absorbent, convex sets. Alternatively they can be defined as a vector space with a family of seminorms, and a topology can be defined in terms of that family. Although in general such spaces are not necessarily normable, the existence of a convex local base for the zero vector is strong enough for the Hahn–Banach theorem to hold, yielding a sufficiently rich theory of continuous linear functionals.
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance in a Euclidean space is defined by a norm on the associated Euclidean vector space, called the Euclidean norm, the 2-norm, or, sometimes, the magnitude or length of the vector. This norm can be defined as the square root of the inner product of a vector with itself.
In linear algebra, a sublinear function, also called a quasi-seminorm or a Banach functional, on a vector space is a real-valued function with only some of the properties of a seminorm. Unlike seminorms, a sublinear function does not have to be nonnegative-valued and also does not have to be absolutely homogeneous. Seminorms are themselves abstractions of the more well known notion of norms, where a seminorm has all the defining properties of a norm except that it is not required to map non-zero vectors to non-zero values.
In mathematics, a homogeneous distribution is a distribution S on Euclidean space Rn or Rn \ {0} that is homogeneous in the sense that, roughly speaking,



















![A homogeneous function is not necessarily continuous, as shown by this example. This is the function
f
{\displaystyle f}
defined by
f
(
x
,
y
)
=
x
{\displaystyle f(x,y)=x}
if
x
y
>
0
{\displaystyle xy>0}
and
f
(
x
,
y
)
=
0
{\displaystyle f(x,y)=0}
if
x
y
<=
0.
{\displaystyle xy\leq 0.}
This function is homogeneous of degree 1, that is,
f
(
s
x
,
s
y
)
=
s
f
(
x
,
y
)
{\displaystyle f(sx,sy)=sf(x,y)}
for any real numbers
s
,
x
,
y
.
{\displaystyle s,x,y.}
It is discontinuous at
y
=
0
,
x
[?]
0.
{\displaystyle y=0,x\neq 0.} HomogeneousDiscontinuousFunction.gif](http://upload.wikimedia.org/wikipedia/commons/thumb/2/21/HomogeneousDiscontinuousFunction.gif/220px-HomogeneousDiscontinuousFunction.gif)












































































































































