
Surfing is a surface water sport in which an individual, a surfer, uses a board to ride on the forward section, or face, of a moving wave of water, which usually carries the surfer towards the shore. Waves suitable for surfing are primarily found on ocean shores, but can also be found in standing waves in the open ocean, in lakes, in rivers in the form of a tidal bore, or in wave pools.
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to a laminar flow, which occurs when a fluid flows in parallel layers, with no disruption between those layers.

The surface layer is the layer of a turbulent fluid most affected by interaction with a solid surface or the surface separating a gas and a liquid where the characteristics of the turbulence depend on distance from the interface. Surface layers are characterized by large normal gradients of tangential velocity and large concentration gradients of any substances transported to or from the interface.

Rogue waves are unusually large, unpredictable, and suddenly appearing surface waves that can be extremely dangerous to ships, even to large ones. They are distinct from tsunamis, which are often almost unnoticeable in deep waters and are caused by the displacement of water due to other phenomena. A rogue wave appearing at the shore is sometimes referred to as a sneaker wave.

In fluid dynamics, a wind wave, water wave, or wind-generated water wave, is a surface wave that occurs on the free surface of bodies of water as a result of the wind blowing over the water's surface. The contact distance in the direction of the wind is known as the fetch. Waves in the oceans can travel thousands of kilometers before reaching land. Wind waves on Earth range in size from small ripples to waves over 30 m (100 ft) high, being limited by wind speed, duration, fetch, and water depth.

Internal waves are gravity waves that oscillate within a fluid medium, rather than on its surface. To exist, the fluid must be stratified: the density must change with depth/height due to changes, for example, in temperature and/or salinity. If the density changes over a small vertical distance, the waves propagate horizontally like surface waves, but do so at slower speeds as determined by the density difference of the fluid below and above the interface. If the density changes continuously, the waves can propagate vertically as well as horizontally through the fluid.

A swell, also sometimes referred to as ground swell, in the context of an ocean, sea or lake, is a series of mechanical waves that propagate along the interface between water and air under the predominating influence of gravity, and thus are often referred to as surface gravity waves. These surface gravity waves have their origin as wind waves, but are the consequence of dispersion of wind waves from distant weather systems, where wind blows for a duration of time over a fetch of water, and these waves move out from the source area at speeds that are a function of wave period and length. More generally, a swell consists of wind-generated waves that are not greatly affected by the local wind at that time. Swell waves often have a relatively long wavelength, as short wavelength waves carry less energy and dissipate faster, but this varies due to the size, strength, and duration of the weather system responsible for the swell and the size of the water body, and varies from event to event, and from the same event, over time. Occasionally, swells that are longer than 700m occur as a result of the most severe storms.

In fluid dynamics, a breaking wave or breaker is a wave whose amplitude reaches a critical level at which large amounts of wave energy transform into turbulent kinetic energy. At this point, simple physical models that describe wave dynamics often become invalid, particularly those that assume linear behaviour.
In acoustics, microbaroms, also known as the "voice of the sea", are a class of atmospheric infrasonic waves generated in marine storms by a non-linear interaction of ocean surface waves with the atmosphere. They typically have narrow-band, nearly sinusoidal waveforms with amplitudes up to a few microbars, and wave periods near 5 seconds. Due to low atmospheric absorption at these low frequencies, microbaroms can propagate thousands of kilometers in the atmosphere, and can be readily detected by widely separated instruments on the Earth's surface.

In hydrodynamics, a clapotis is a non-breaking standing wave pattern, caused for example, by the reflection of a traveling surface wave train from a near vertical shoreline like a breakwater, seawall or steep cliff. The resulting clapotic wave does not travel horizontally, but has a fixed pattern of nodes and antinodes. These waves promote erosion at the toe of the wall, and can cause severe damage to shore structures. The term was coined in 1877 by French mathematician and physicist Joseph Valentin Boussinesq who called these waves 'le clapotis' meaning "the lapping".

In fluid dynamics, wave shoaling is the effect by which surface waves, entering shallower water, change in wave height. It is caused by the fact that the group velocity, which is also the wave-energy transport velocity, changes with water depth. Under stationary conditions, a decrease in transport speed must be compensated by an increase in energy density in order to maintain a constant energy flux. Shoaling waves will also exhibit a reduction in wavelength while the frequency remains constant.
In seismology, a microseism is defined as a faint earth tremor caused by natural phenomena. Sometimes referred to as a "hum", it should not be confused with the anomalous acoustic phenomenon of the same name. The term is most commonly used to refer to the dominant background seismic and electromagnetic noise signals on Earth, which are caused by water waves in the oceans and lakes. Characteristics of microseism are discussed by Bhatt. Because the ocean wave oscillations are statistically homogenous over several hours, the microseism signal is a long-continuing oscillation of the ground. The most energetic seismic waves that make up the microseismic field are Rayleigh waves, but Love waves can make up a significant fraction of the wave field, and body waves are also easily detected with arrays. Because the conversion from the ocean waves to the seismic waves is very weak, the amplitude of ground motions associated to microseisms does not generally exceed 10 micrometers.
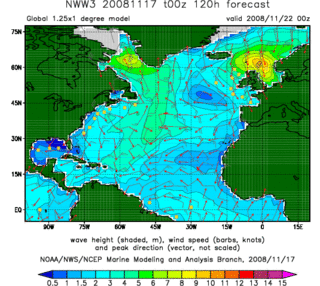
In fluid dynamics, wind wave modeling describes the effort to depict the sea state and predict the evolution of the energy of wind waves using numerical techniques. These simulations consider atmospheric wind forcing, nonlinear wave interactions, and frictional dissipation, and they output statistics describing wave heights, periods, and propagation directions for regional seas or global oceans. Such wave hindcasts and wave forecasts are extremely important for commercial interests on the high seas. For example, the shipping industry requires guidance for operational planning and tactical seakeeping purposes.
In fluid dynamics, the Coriolis–Stokes force is a forcing of the mean flow in a rotating fluid due to interaction of the Coriolis effect and wave-induced Stokes drift. This force acts on water independently of the wind stress.
Internal tides are generated as the surface tides move stratified water up and down sloping topography, which produces a wave in the ocean interior. So internal tides are internal waves at a tidal frequency. The other major source of internal waves is the wind which produces internal waves near the inertial frequency. When a small water parcel is displaced from its equilibrium position, it will return either downwards due to gravity or upwards due to buoyancy. The water parcel will overshoot its original equilibrium position and this disturbance will set off an internal gravity wave. Munk (1981) notes, "Gravity waves in the ocean's interior are as common as waves at the sea surface-perhaps even more so, for no one has ever reported an interior calm."

Infragravity waves are surface gravity waves with frequencies lower than the wind waves – consisting of both wind sea and swell – thus corresponding with the part of the wave spectrum lower than the frequencies directly generated by forcing through the wind.
In fluid dynamics, wave setup is the increase in mean water level due to the presence of breaking waves. Similarly, wave setdown is a wave-induced decrease of the mean water level before the waves break. For short, the whole phenomenon is often denoted as wave setup, including both increase and decrease of mean elevation. This setup is primarily present in and near the coastal surf zone. Besides a spatial variation in the (mean) wave setup, also a variation in time may be present – known as surf beat – causing infragravity wave radiation.
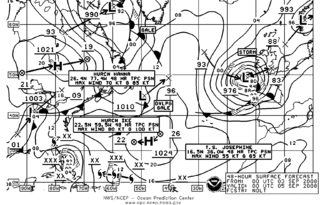
Marine weather forecasting is the process by which mariners and meteorological organizations attempt to forecast future weather conditions over the Earth's oceans. Mariners have had rules of thumb regarding the navigation around tropical cyclones for many years, dividing a storm into halves and sailing through the normally weaker and more navigable half of their circulation. Marine weather forecasts by various weather organizations can be traced back to the sinking of the Royal Charter in 1859 and the RMS Titanic in 1912.
The nonlinearity of surface gravity waves refers to their deviations from a sinusoidal shape. In the fields of physical oceanography and coastal engineering, the two categories of nonlinearity are skewness and asymmetry. Wave skewness and asymmetry occur when waves encounter an opposing current or a shallow area. As waves shoal in the nearshore zone, in addition to their wavelength and height changing, their asymmetry and skewness also change. Wave skewness and asymmetry are often implicated in ocean engineering and coastal engineering for the modelling of random sea states, in particular regarding the distribution of wave height, wavelength and crest length. For practical engineering purposes, it is important to know the probability of these wave characteristics in seas and oceans at a given place and time. This knowledge is crucial for the prediction of extreme waves, which are a danger for ships and offshore structures. Satellite altimeter Envisat RA-2 data shows geographically coherent skewness fields in the ocean and from the data has been concluded that large values of skewness occur primarily in regions of large significant wave height.

Internal wave breaking is a process during which internal gravity waves attain a large amplitude compared to their length scale, become nonlinearly unstable and finally break. This process is accompanied by turbulent dissipation and mixing. As internal gravity waves carry energy and momentum from the environment of their inception, breaking and subsequent turbulent mixing affects the fluid characteristics in locations of breaking. Consequently, internal wave breaking influences even the large scale flows and composition in both the ocean and the atmosphere. In the atmosphere, momentum deposition by internal wave breaking plays a key role in atmospheric phenomena such as the Quasi-Biennial Oscillation and the Brewer-Dobson Circulation. In the deep ocean, mixing induced by internal wave breaking is an important driver of the meridional overturning circulation. On smaller scales, breaking-induced mixing is important for sediment transport and for nutrient supply to the photic zone. Most breaking of oceanic internal waves occurs in continental shelves, well below the ocean surface, which makes it a difficult phenomenon to observe.















