
Area is the measure of a region's size on a surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid . Two different regions may have the same area ; by synecdoche, "area" sometimes is used to refer to the region, as in a "polygonal area".
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.

In mathematics, a linear equation is an equation that may be put in the form where are the variables, and are the coefficients, which are often real numbers. The coefficients may be considered as parameters of the equation and may be arbitrary expressions, provided they do not contain any of the variables. To yield a meaningful equation, the coefficients are required to not all be zero.

In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
In algebra, a quadratic equation is any equation that can be rearranged in standard form as

In common usage, the abscissa refers to the x coordinate and the ordinate refers to the y coordinate of a standard two-dimensional graph.

In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio. The ratio is called coefficient of proportionality and its reciprocal is known as constant of normalization. Two sequences are inversely proportional if corresponding elements have a constant product, also called the coefficient of proportionality.

In mathematics, the graph of a function is the set of ordered pairs , where In the common case where and are real numbers, these pairs are Cartesian coordinates of points in a plane and often form a curve. The graphical representation of the graph of a function is also known as a plot.

In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry.

In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before the 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so "quadratic polynomial" and "quadratic function" were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as "quadratic".

In Euclidean geometry, a translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction. A translation can also be interpreted as the addition of a constant vector to every point, or as shifting the origin of the coordinate system. In a Euclidean space, any translation is an isometry.

In mathematics, a cubic function is a function of the form that is, a polynomial function of degree three. In many texts, the coefficientsa, b, c, and d are supposed to be real numbers, and the function is considered as a real function that maps real numbers to real numbers or as a complex function that maps complex numbers to complex numbers. In other cases, the coefficients may be complex numbers, and the function is a complex function that has the set of the complex numbers as its codomain, even when the domain is restricted to the real numbers.
Many letters of the Latin alphabet, both capital and small, are used in mathematics, science, and engineering to denote by convention specific or abstracted constants, variables of a certain type, units, multipliers, or physical entities. Certain letters, when combined with special formatting, take on special meaning.

Symmetry occurs not only in geometry, but also in other branches of mathematics. Symmetry is a type of invariance: the property that a mathematical object remains unchanged under a set of operations or transformations.
In mathematics, a variable is a symbol that represents a mathematical object. A variable may represent a number, a vector, a matrix, a function, the argument of a function, a set, or an element of a set.
In mathematics, the word constant conveys multiple meanings. As an adjective, it refers to non-variance ; as a noun, it has two different meanings:
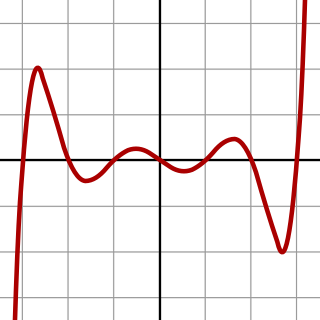
In algebra, a septic equation is an equation of the form
In Euclidean and projective geometry, five points determine a conic, just as two (distinct) points determine a line. There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.
























