Year loss table

Last updated

A Year Loss Table (YLT) is a list of historical or simulated years, with financial losses for each year. [1] [2] [3] YLTs are widely used in catastrophe modeling, as a way to record and communicate historical or simulated losses from catastrophes. The use of lists of years with historical or simulated financial losses is discussed in many references on catastrophe modelling and disaster risk management, [4] [5] [6] [7] [8] [9] but it is only more recently that the name YLT has become standard. [1] [2] [3]

Contents

Overview

Year of interest

In a simulated YLT, each year of simulated loss is considered a possible loss outcome for a single year, the year of interest, which is usually in the future. In insurance industry catastrophe modelling, the year of interest is often this year or next year, due to the annual nature of many insurance contracts. [1] However, the year can also be defined to be any year in the past or the future.

Events

Many YLTs are event based i.e., they are constructed from historical or simulated catastrophe events, each of which has an associated loss. Each event is allocated to one or more years in the YLT and there may be multiple events in a year. [4] [5] [6] The events may have an associated frequency model, that specifies the distribution for the number of different types of events per year, and an associated severity distribution, that specifies the distribution of loss for each event.

Events in an event-based YLT may all be of one peril-type (such as hurricane) or may be a mixture of peril-types (such as hurricane and earthquake).

Period Loss Tables (PLTs)

YLTs represent the possible losses in a period of one year, but can be generalized to represent the possible losses in any length of time, in which case they may be referred to as Period Loss Tables (PLTs).

Use in insurance

YLTs are widely used in the insurance industry, [1] [2] because they are a flexible way to store samples from a distribution of possible losses. Two properties, in particular, make them useful:

Examples of YLTs

YLTs are often stored in either long-form or short-form.

Example of a long-form YLT

In a long-form YLT, [1] each row of the YLT corresponds to a different loss-causing event. For each event, the YLT records the year, the event, the loss, and any other relevant information about the event.

YearEvent IDsEvent Loss
1965$100,000
17$1,000,000
2432$400,000
3--
.........
100,0007$1,000,000
100,000300,001$2,000,000
100,0002$3,000,000

In this example:

Example of a short-form YLT

In a short-form YLT, [3] each row of the YLT corresponds to a different year. For each event, the YLT records the year, the loss, and any other relevant information about the year.

The same YLT as above, but condensed to short-form, would look like:

YearAnnual Total Loss
1$1,100,000
2$400,000
3$0
......
100,000$6,000,000

Frequency models

Poisson distribution

The most commonly used frequency model for the events in a YLT is Poisson distribution with constant parameters. [6]

Mixed poisson distribution

An alternative frequency model is the mixed Poisson distribution, which allows for temporal and spatial clustering of events. [10]

Weighted YLTs (WYLTs)

YLTs can be generalized to weighted YLTs (WYLTs) by adding weights to the years. [11] The weights would typically sum to 1.

YearEvent LossWeight
1$1,100,0000.0001
2$400,0000.0002
3$00.00001
.........
100,000$6,000,0000.0003

Stochastic parameter YLTs

When YLTs are generated from parametrized mathematical models, they may use the same parameter values in each year (fixed parameter YLTs), or different parameter values in each year (stochastic parameter YLTs). [3] In a stochastic parameter YLT the parameters used in each year would typically themselves be generated from some underlying distribution, which could be a Bayesian posterior distribution for the parameter. Varying the parameters from year to year in a stochastic parameter YLT is a way to incorporate epistemic uncertainty into the YLT.

As an example, the annual frequency of hurricanes hitting the United States might be modelled as a Poisson distribution with an estimated mean of 1.67 hurricanes per year. The estimation uncertainty around the estimate of the mean might considered to be a gamma distribution. In a fixed parameter YLT, the number of hurricanes in every year would be simulated using a Poisson distribution with a mean of 1.67 hurricanes per year, and the distribution of estimation uncertainty would be ignored. In a stochastic parameter YLT, the number of hurricanes in each year would be simulated by first simulating the mean number of hurricanes for that year from the gamma distribution, and then simulating the number of hurricanes itself from a Poisson distribution with the simulated mean.

In the fixed parameter YLT the mean of the Poisson distribution used to model the frequency of hurricanes, by year, would be:

YearPoisson mean
11.67
21.67
31.67
......
100,0001.67

In the stochastic parameter YLT the mean of the Poisson distribution used to model the frequency of hurricanes, by year, might be:

YearPoisson mean
11.70
21.62
31.81
......
100,0001.68

Adjusting YLTs and WYLTs

It is often of interest to adjust YLTs, to perform sensitivity tests, or to make adjustments for climate change. Adjustments can be made in a number of different ways.

Resimulation with different frequencies

If a YLT has been created by simulating from a list of events with given frequencies, then one simple way to adjust the YLT is to resimulate but with different frequencies.

Incremental simulation

Resimulation with different frequencies can be made much more accurate by using the incremental simulation approach. [12]

Weighting

YLTs can be adjusted by applying weights to the years, which converts a YLT to a WYLT. An example would be adjusting weather and climate risk YLTs to account for the effects of climate variability and change. [11] [13] By putting more weights on some years and less on others, the implied distribution of events changes, and the distributions of event loss and annual loss change accordingly.

Adjusting an existing YLT to represent a different view of risk, as opposed to rebuilding the YLT from scratch, may have the benefit that it avoids having to resimulate the events, the positions of the events in the years, and the losses for each event and each year. This may be more efficient.

YLT importance sampling

One general and principled method for applying weights to YLTs is importance sampling [11] [3] in which the weight on the year is given by the ratio of the probability of year in the adjusted model to the probability of year in the unadjusted model. Importance sampling can be applied to both fixed parameter YLTs [11] and stochastic parameter YLTs. [3]

Repeat and delete

WYLTs are less flexible, in some ways, than YLTs. For instance, two WYLTs, with different weights, cannot easily be combined to create a single new WYLT. For this reason, it may be useful to convert WYLTs to YLTs. This can be done using the method of repeat-and-delete, [11] in which years with high weights are repeated one or more times, and years with low weights are deleted.

Calculating metrics from YLTs and WYLTs

Standard risk metrics can be calculated straightforwardly from YLTs and WYLTs. [1] Examples would be:

Related Research Articles

A parameter, generally, is any characteristic that can help in defining or classifying a particular system. That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc.

<span class="mw-page-title-main">Uncertainty</span> Situations involving imperfect or unknown information

Uncertainty or Incertitude refers to epistemic situations involving imperfect or unknown information. It applies to predictions of future events, to physical measurements that are already made, or to the unknown. Uncertainty arises in partially observable or stochastic environments, as well as due to ignorance, indolence, or both. It arises in any number of fields, including insurance, philosophy, physics, statistics, economics, finance, medicine, psychology, sociology, engineering, metrology, meteorology, ecology and information science.

Monte Carlo methods are used in corporate finance and mathematical finance to value and analyze (complex) instruments, portfolios and investments by simulating the various sources of uncertainty affecting their value, and then determining the distribution of their value over the range of resultant outcomes. This is usually done by help of stochastic asset models. The advantage of Monte Carlo methods over other techniques increases as the dimensions of the problem increase.

In the field of information retrieval, divergence from randomness, one of the first models, is one type of probabilistic model. It is basically used to test the amount of information carried in the documents. It is based on Harter's 2-Poisson indexing-model. The 2-Poisson model has a hypothesis that the level of the documents is related to a set of documents which contains words occur relatively greater than the rest of the documents. It is not a 'model', but a framework for weighting terms using probabilistic methods, and it has a special relationship for term weighting based on notion of eliteness.

Catastrophe modeling is the process of using computer-assisted calculations to estimate the losses that could be sustained due to a catastrophic event such as a hurricane or earthquake. Cat modeling is especially applicable to analyzing risks in the insurance industry and is at the confluence of actuarial science, engineering, meteorology, and seismology.

Probabilistic risk assessment (PRA) is a systematic and comprehensive methodology to evaluate risks associated with a complex engineered technological entity or the effects of stressors on the environment.

<span class="mw-page-title-main">Ensemble forecasting</span> Multiple simulation method for weather forecasting

Ensemble forecasting is a method used in or within numerical weather prediction. Instead of making a single forecast of the most likely weather, a set of forecasts is produced. This set of forecasts aims to give an indication of the range of possible future states of the atmosphere. Ensemble forecasting is a form of Monte Carlo analysis. The multiple simulations are conducted to account for the two usual sources of uncertainty in forecast models: (1) the errors introduced by the use of imperfect initial conditions, amplified by the chaotic nature of the evolution equations of the atmosphere, which is often referred to as sensitive dependence on initial conditions; and (2) errors introduced because of imperfections in the model formulation, such as the approximate mathematical methods to solve the equations. Ideally, the verified future atmospheric state should fall within the predicted ensemble spread, and the amount of spread should be related to the uncertainty (error) of the forecast. In general, this approach can be used to make probabilistic forecasts of any dynamical system, and not just for weather prediction.

In statistics, Poisson regression is a generalized linear model form of regression analysis used to model count data and contingency tables. Poisson regression assumes the response variable Y has a Poisson distribution, and assumes the logarithm of its expected value can be modeled by a linear combination of unknown parameters. A Poisson regression model is sometimes known as a log-linear model, especially when used to model contingency tables.

<span class="mw-page-title-main">Catastrophe bond</span>

Catastrophe bonds are risk-linked securities that transfer a specified set of risks from a sponsor to investors. They were created and first used in the mid-1990s in the aftermath of Hurricane Andrew and the Northridge earthquake.

"Stochastic" means being or having a random variable. A stochastic model is a tool for estimating probability distributions of potential outcomes by allowing for random variation in one or more inputs over time. The random variation is usually based on fluctuations observed in historical data for a selected period using standard time-series techniques. Distributions of potential outcomes are derived from a large number of simulations which reflect the random variation in the input(s).

In statistics, overdispersion is the presence of greater variability in a data set than would be expected based on a given statistical model.

A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.

Quantification of Margins and Uncertainty (QMU) is a decision support methodology for complex technical decisions. QMU focuses on the identification, characterization, and analysis of performance thresholds and their associated margins for engineering systems that are evaluated under conditions of uncertainty, particularly when portions of those results are generated using computational modeling and simulation. QMU has traditionally been applied to complex systems where comprehensive experimental test data is not readily available and cannot be easily generated for either end-to-end system execution or for specific subsystems of interest. Examples of systems where QMU has been applied include nuclear weapons performance, qualification, and stockpile assessment. QMU focuses on characterizing in detail the various sources of uncertainty that exist in a model, thus allowing the uncertainty in the system response output variables to be well quantified. These sources are frequently described in terms of probability distributions to account for the stochastic nature of complex engineering systems. The characterization of uncertainty supports comparisons of design margins for key system performance metrics to the uncertainty associated with their calculation by the model. QMU supports risk-informed decision-making processes where computational simulation results provide one of several inputs to the decision-making authority. There is currently no standardized methodology across the simulation community for conducting QMU; the term is applied to a variety of different modeling and simulation techniques that focus on rigorously quantifying model uncertainty in order to support comparison to design margins.

<span class="mw-page-title-main">Hydrological model</span>

A hydrologic model is a simplification of a real-world system that aids in understanding, predicting, and managing water resources. Both the flow and quality of water are commonly studied using hydrologic models.

Complete spatial randomness (CSR) describes a point process whereby point events occur within a given study area in a completely random fashion. It is synonymous with a homogeneous spatial Poisson process. Such a process is modeled using only one parameter , i.e. the density of points within the defined area. The term complete spatial randomness is commonly used in Applied Statistics in the context of examining certain point patterns, whereas in most other statistical contexts it is referred to the concept of a spatial Poisson process.

In geophysics, seismic inversion is the process of transforming seismic reflection data into a quantitative rock-property description of a reservoir. Seismic inversion may be pre- or post-stack, deterministic, random or geostatistical; it typically includes other reservoir measurements such as well logs and cores.

<span class="mw-page-title-main">Risk</span> The possibility of something bad happening

In simple terms, risk is the possibility of something bad happening. Risk involves uncertainty about the effects/implications of an activity with respect to something that humans value, often focusing on negative, undesirable consequences. Many different definitions have been proposed. The international standard definition of risk for common understanding in different applications is "effect of uncertainty on objectives".

<span class="mw-page-title-main">Poisson point process</span> Type of random mathematical object

In probability, statistics and related fields, a Poisson point process is a type of random mathematical object that consists of points randomly located on a mathematical space with the essential feature that the points occur independently of one another. The Poisson point process is also called a Poisson random measure, Poisson random point field or Poisson point field. When the process is defined on the real line, it is often called simply the Poisson process.

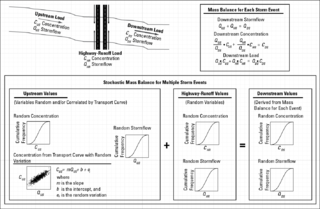
<span class="mw-page-title-main">Stochastic empirical loading and dilution model</span>

The stochastic empirical loading and dilution model (SELDM) is a stormwater quality model. SELDM is designed to transform complex scientific data into meaningful information about the risk of adverse effects of runoff on receiving waters, the potential need for mitigation measures, and the potential effectiveness of such management measures for reducing these risks. The U.S. Geological Survey developed SELDM in cooperation with the Federal Highway Administration to help develop planning-level estimates of event mean concentrations, flows, and loads in stormwater from a site of interest and from an upstream basin. SELDM uses information about a highway site, the associated receiving-water basin, precipitation events, stormflow, water quality, and the performance of mitigation measures to produce a stochastic population of runoff-quality variables. Although SELDM is, nominally, a highway runoff model is can be used to estimate flows concentrations and loads of runoff-quality constituents from other land use areas as well. SELDM was developed by the U.S. Geological Survey so the model, source code, and all related documentation are provided free of any copyright restrictions according to U.S. copyright laws and the USGS Software User Rights Notice. SELDM is widely used to assess the potential effect of runoff from highways, bridges, and developed areas on receiving-water quality with and without the use of mitigation measures. Stormwater practitioners evaluating highway runoff commonly use data from the Highway Runoff Database (HRDB) with SELDM to assess the risks for adverse effects of runoff on receiving waters.

References

  1. 1 2 3 4 5 6 Jones, M; Mitchell-Wallace, K; Foote, M; Hillier, J (2017). "Fundamentals". In Mitchell-Wallace, K; Jones, M; Hillier, J; Foote, M (eds.). Natural Catastrophe Risk Management and Modelling. Wiley. p. 36. doi:10.1002/9781118906057. ISBN   9781118906057.
  2. 1 2 3 Yiptong, A; Michel, G (2018). "Portfolio Optimisation using Catastrophe Model Results". In Michel, G (ed.). Risk Modelling for Hazards and Disasters. Elsevier. p. 249.
  3. 1 2 3 4 5 6 Jewson, S. (2022). "Application of Uncertain Hurricane Climate Change Projections to Catastrophe Risk Models". Stochastic Environmental Research and Risk Assessment. 36 (10): 3355–3375. doi:10.1007/s00477-022-02198-y. S2CID   247623520.
  4. 1 2 Friedman, D. (1972). "Insurance and the Natural Hazards". ASTIN. 7: 4–58. doi: 10.1017/S0515036100005699 . S2CID   156431336.
  5. 1 2 Friedman, D. (1975). Computer Simulation in Natural Hazard Assessment. University of Colorado.
  6. 1 2 3 Clark, K. (1986). "A Formal Approach to Catastrophe Risk Assessment and Management". Proceedings of the American Casualty Actuarial Society. 73 (2).
  7. ↑ Woo, G. (2011). Calculating Catastrophe. Imperial College Press. p. 127.
  8. ↑ Edwards, T; Challenor, P (2013). "Risk and Uncertainty in Hydrometeorological Hazards". In Rougier, J; Sparks, S; Hill, L (eds.). Risk and Uncertainty Assessment for Natural Hazards. Cambridge. p. 120.
  9. ↑ Simmons, D (2017). "Qualitative and Quantitative Approaches to Risk Assessment". In Poljansek, K; Ferrer, M; De Groeve, T; Clark, I (eds.). Science for Disaster Risk Management. European Commission. p. 54.
  10. ↑ Khare, S.; Bonazzi, A.; Mitas, C.; Jewson, S. (2015). "Modelling Clustering of Natural Hazard Phenomena and the Effect on Re/insurance Loss Perspectives". Natural Hazards and Earth System Sciences. 15 (6): 1357–1370. Bibcode:2015NHESS..15.1357K. doi: 10.5194/nhess-15-1357-2015 .
  11. 1 2 3 4 5 Jewson, S.; Barnes, C.; Cusack, S.; Bellone, E. (2019). "Adjusting Catastrophe Model Ensembles using Importance Sampling, with Application to Damage Estimation for Varying Levels of Hurricane Activity". Meteorological Applications. 27. doi: 10.1002/met.1839 . S2CID   202765343.
  12. ↑ Jewson, S. (2023). "A new simulation algorithm for more precise estimates of change in catastrophe risk models, with application to hurricanes and climate change". Stochastic Environmental Research and Risk Assessment. doi:10.1007/s00477-023-02409-0.
  13. ↑ Sassi, M.; et al. (2019). "Impact of Climate Change on European Winter and Summer Flood Losses". Advances in Water Resources. 129: 165–177. Bibcode:2019AdWR..129..165S. doi:10.1016/j.advwatres.2019.05.014. hdl: 10852/74923 . S2CID   182595162.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.