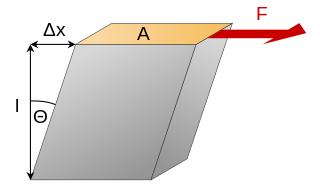
Cubic materials
Cubic materials are special orthotropic materials that are invariant with respect to 90° rotations with respect to the principal axes, i.e., the material is the same along its principal axes. Due to these additional symmetries the stiffness tensor can be written with just three different material properties like

The inverse of this matrix is commonly written as [3]

where  is the Young's modulus,
is the Young's modulus,  is the shear modulus, and
is the shear modulus, and  is the Poisson's ratio. Therefore, we can think of the ratio as the relation between the shear modulus for the cubic material and its (isotropic) equivalent:
is the Poisson's ratio. Therefore, we can think of the ratio as the relation between the shear modulus for the cubic material and its (isotropic) equivalent:

Tensorial Anisotropy Index
The Tensorial Anisotropy Index AT [5] extends the Zener ratio for fully anisotropic materials and overcomes the limitation of the AU that is designed for materials exhibiting internal symmetries of elastic crystals, which is not always observed in multi-component composites. It takes into consideration all the 21 coefficients of the fully anisotropic stiffness tensor and covers the directional differences among the stiffness tensor groups.
It is composed of two major parts  and
and  , the former referring to components existing in cubic tensor and the latter in anisotropic tensor so that
, the former referring to components existing in cubic tensor and the latter in anisotropic tensor so that  This first component includes the modified Zener ratio and additionally accounts for directional differences in the material, which exist in orthotropic material, for instance. The second component of this index
This first component includes the modified Zener ratio and additionally accounts for directional differences in the material, which exist in orthotropic material, for instance. The second component of this index  covers the influence of stiffness coefficients that are nonzero only for non-cubic materials and remains zero otherwise.
covers the influence of stiffness coefficients that are nonzero only for non-cubic materials and remains zero otherwise.

where  is the coefficient of variation for each stiffness group accounting for directional differences of material stiffness, i.e.
is the coefficient of variation for each stiffness group accounting for directional differences of material stiffness, i.e.  In cubic materials each stiffness component in groups 1-3 has equal value and thus this expression reduces directly to Zener ratio for cubic materials.
In cubic materials each stiffness component in groups 1-3 has equal value and thus this expression reduces directly to Zener ratio for cubic materials.
The second component of this index  is non-zero for complex materials or composites with only few or no symmetries in their internal structure. In such cases the remaining stiffness coefficients joined in three groups are not null
is non-zero for complex materials or composites with only few or no symmetries in their internal structure. In such cases the remaining stiffness coefficients joined in three groups are not null