Antimatter tests of Lorentz violation

Last updated

High-precision experiments could reveal small previously unseen differences between the behavior of matter and antimatter. This prospect is appealing to physicists because it may show that nature is not Lorentz symmetric.

Contents

Introduction

Ordinary matter is made up of protons, electrons, and neutrons. The quantum behavior of these particles can be predicted with excellent accuracy using the Dirac equation, named after P.A.M. Dirac. One of the triumphs of the Dirac equation is its prediction of the existence of antimatter particles. Antiprotons, positrons, and antineutrons are now well understood, and can be created and studied in experiments.

High-precision experiments have been unable to detect any difference between the masses of particles and those of the corresponding antiparticles. They also have been unable to detect any difference between the magnitudes of the charges, or between the lifetimes, of particles and antiparticles. These mass, charge, and lifetime symmetries are required in a Lorentz and CPT symmetric universe, but are only a small number of the properties that need to match if the universe is Lorentz and CPT symmetric.

The Standard-Model Extension (SME), a comprehensive theoretical framework for Lorentz and CPT violation, makes specific predictions about how particles and antiparticles would behave differently in a universe that is very close to, but not exactly, Lorentz symmetric. [1] [2] [3] In loose terms, the SME can be visualized as being constructed from fixed background fields that interact weakly, but differently, with particles and antiparticles.

The behavioral differences between matter and antimatter are specific to each individual experiment. Factors that determine the behavior include the particle species involved, the electromagnetic, gravitational, and nuclear fields controlling the system. Furthermore, for any Earth-bound experiment, the rotational and orbital motion of the Earth is important, leading to sidereal and seasonal signals. For experiments conducted in space, the orbital motion of the craft is an important factor in determining the signals of Lorentz violation that might arise. To harness the predictive power of the SME in any specific system, a calculation has to be performed so that all these factors can be accounted for. These calculations are facilitated by the reasonable assumption that Lorentz violations, if they exist, are small. This makes it possible to use perturbation theory to obtain results that would otherwise be extremely difficult to find.

The SME generates a modified Dirac equation that breaks Lorentz symmetry for some types of particle motions, but not others. It therefore holds important information about how Lorentz violations might have been hidden in past experiments, or might be revealed in future ones.

Lorentz violation tests with Penning Traps

A Penning trap is a research apparatus capable of trapping individual charged particles and their antimatter counterparts. The trapping mechanism is a strong magnetic field that keeps the particles near a central axis, and an electric field that turns the particles around when they stray too far along the axis. The motional frequencies of the trapped particle can be monitored and measured with astonishing precision. One of these frequencies is the anomaly frequency, which has played an important role in the measurement of the gyromagnetic ratio of the electron (see gyromagnetic ratio § gyromagnetic ratio for an isolated electron).

The first calculations of SME effects in Penning traps were published in 1997 and 1998. [4] [5] They showed that, in identical Penning traps, if the anomaly frequency of an electron was increased, then the anomaly frequency of a positron would be decreased. The size of the increase or decrease in the frequency would be a measure of the strength of one of the SME background fields. More specifically, it is a measure of the component of the background field along the direction of the axial magnetic field.

In tests of Lorentz symmetry, the noninertial nature of the laboratory due to the rotational and orbital motion of the Earth has to be taken into account. Each Penning-trap measurement is the projection of the background SME fields along the axis of the experimental magnetic field at the time of the experiment. This is further complicated if the experiment takes hours, days, or longer to perform.

One approach is to seek instantaneous differences, by comparing anomaly frequencies for a particle and an antiparticle measured at the same time on different days. Another approach is to seek sidereal variations, by continuously monitoring the anomaly frequency for just one species of particle over an extended time. Each offers different challenges. For example, instantaneous comparisons require the electric field in the trap to be precisely reversed, while sidereal tests are limited by the stability of the magnetic field.

An experiment conducted by the physicist Gerald Gabrielse of Harvard University involved two particles confined in a Penning trap. The idea was to compare a proton and an antiproton, but to overcome the technicalities of having opposite charges, a negatively charged hydrogen ion was used in place of the proton. The ion, two electrons bound electrostatically with a proton, and the antiproton have the same charge and can therefore be simultaneously trapped. This design allows for quick interchange of the proton and the antiproton and so an instantaneous-type Lorentz test can be performed. The cyclotron frequencies of the two trapped particles were about 90 MHz, and the apparatus was capable of resolving differences in these of about 1.0 Hz. The absence of Lorentz violating effects of this type placed a limit on combinations of -type SME coefficients that had not been accessed in other experiments. The results [6] appeared in Physical Review Letters in 1999.

The Penning-trap group at the University of Washington, headed by the Nobel Laureate Hans Dehmelt, conducted a search for sidereal variations in the anomaly frequency of a trapped electron. The results were extracted from an experiment that ran for several weeks, and the analysis required splitting the data into "bins" according to the orientation of the apparatus in the inertial reference frame of the Sun. At a resolution of 0.20 Hz, they were unable to discern any sidereal variations in the anomaly frequency, which runs around 185,000,000 Hz. Translating this into an upper bound on the relevant SME background field, places a bound of about 10−24 GeV on a -type electron coefficient. This work [7] was published in Physical Review Letters in 1999.

Another experimental result from the Dehmelt group involved a comparison of the instantaneous type. Using data from a single trapped electron and a single trapped positron, they again found no difference between the two anomaly frequencies at a resolution of about 0.2 Hz. This result placed a bound on a simpler combination of -type coefficients at a level of about 10−24 GeV. In addition to being a limit on Lorentz violation, this also limits the CPT violation. This result [8] appeared in Physical Review Letters in 1999.

Lorentz violation in antihydrogen

The antihydrogen atom is the antimatter counterpart of the hydrogen atom. It has a negatively charged antiproton at the nucleus that attracts a positively charged positron orbiting around it.

The spectral lines of hydrogen have frequencies determined by the energy differences between the quantum-mechanical orbital states of the electron. These lines have been studied in thousands of spectroscopic experiments and are understood in great detail. The quantum mechanics of the positron orbiting an antiproton in the antihydrogen atom is expected to be very similar to that of the hydrogen atom. In fact, conventional physics predicts that the spectrum of antihydrogen is identical to that of regular hydrogen.

In the presence of the background fields of the SME, the spectra of hydrogen and antihydrogen are expected to show tiny differences in some lines, and no differences in others. Calculations of these SME effects in antihydrogen and hydrogen were published [9] in Physical Review Letters in 1999. One of the main results found is that hyperfine transitions are sensitive to Lorentz breaking effects.

Several experimental groups at CERN are working on producing antihydrogen: AEGIS, ALPHA, ASACUSA, ATRAP, and GBAR.

Creating trapped antihydrogen in sufficient quantities to do spectroscopy is an enormous experimental challenge. Signatures of Lorentz violation are similar to those expected in Penning traps. There would be sidereal effects causing variations in the spectral frequencies as the experimental laboratory turns with the Earth. There would also be the possibility of finding instantaneous Lorentz breaking signals when antihydrogen spectra are compared directly with conventional hydrogen spectra

In October 2017, the BASE experiment at CERN reported a measurement of the antiproton magnetic moment to a precision of 1.5 parts per billion. [10] [11] It is consistent with the most precise measurement of the proton magnetic moment (also made by BASE in 2014), which supports the hypothesis of CPT symmetry. This measurement represents the first time that a property of antimatter is known more precisely than the equivalent property in matter.

Lorentz violation with muons

The muon and its positively charged antiparticle have been used to perform tests of Lorentz symmetry. Since the lifetime of the muon is only a few microseconds, the experiments are quite different from ones with electrons and positrons. Calculations for muon experiments aimed at probing Lorentz violation in the SME were first published in the year 2000. [12]

In the year 2001, Hughes and collaborators published their results from a search for sidereal signals in the spectrum of muonium, an atom consisting of an electron bound to a negatively charged muon. Their data, taken over a two-year period, showed no evidence for Lorentz violation. This placed a stringent constraint on a combination of -type coefficients in the SME, published in Physical Review Letters. [13]

In 2008, the Muon Collaboration at the Brookhaven National Laboratory published results after searching for signals of Lorentz violation with muons and antimuons. In one type of analysis, they compared the anomaly frequencies for the muon and its antiparticle. In another, they looked for sidereal variations by allocating their data into one-hour "bins" according to the orientation of the Earth relative to the Sun-centered inertial reference frame. Their results, published in Physical Review Letters in 2008, [14] show no signatures of Lorentz violation at the resolution of the Brookhaven experiment.

Experimental results in all sectors of the SME are summarized in the Data Tables for Lorentz and CPT violation. [15]

See also

Related Research Articles

<span class="mw-page-title-main">Antimatter</span> Material composed of antiparticles of the corresponding particles of ordinary matter

In modern physics, antimatter is defined as matter composed of the antiparticles of the corresponding particles in "ordinary" matter, and can be thought of as matter with reversed charge, parity, and time, known as CPT reversal. Antimatter occurs in natural processes like cosmic ray collisions and some types of radioactive decay, but only a tiny fraction of these have successfully been bound together in experiments to form antiatoms. Minuscule numbers of antiparticles can be generated at particle accelerators; however, total artificial production has been only a few nanograms. No macroscopic amount of antimatter has ever been assembled due to the extreme cost and difficulty of production and handling.

<span class="mw-page-title-main">Positron</span> Subatomic particle

The positron or antielectron is the antiparticle or the antimatter counterpart of the electron. It has an electric charge of +1 e, a spin of 1/2, and the same mass as an electron. When a positron collides with an electron, annihilation occurs. If this collision occurs at low energies, it results in the production of two or more photons.

<span class="mw-page-title-main">Antihydrogen</span> Exotic particle made of an antiproton and positron

Antihydrogen is the antimatter counterpart of hydrogen. Whereas the common hydrogen atom is composed of an electron and proton, the antihydrogen atom is made up of a positron and antiproton. Scientists hope that studying antihydrogen may shed light on the question of why there is more matter than antimatter in the observable universe, known as the baryon asymmetry problem. Antihydrogen is produced artificially in particle accelerators.

Charge, parity, and time reversal symmetry is a fundamental symmetry of physical laws under the simultaneous transformations of charge conjugation (C), parity transformation (P), and time reversal (T). CPT is the only combination of C, P, and T that is observed to be an exact symmetry of nature at the fundamental level. The CPT theorem says that CPT symmetry holds for all physical phenomena, or more precisely, that any Lorentz invariant local quantum field theory with a Hermitian Hamiltonian must have CPT symmetry.

ATHENA, also known as the AD-1 experiment, was an antimatter research project at the Antiproton Decelerator at CERN, Geneva. In August 2002, it was the first experiment to produce 50,000 low-energy antihydrogen atoms, as reported in Nature. In 2005, ATHENA was disbanded and many of the former members of the research team worked on the subsequent ALPHA experiment.

This is a timeline of subatomic particle discoveries, including all particles thus far discovered which appear to be elementary given the best available evidence. It also includes the discovery of composite particles and antiparticles that were of particular historical importance.

<span class="mw-page-title-main">MiniBooNE</span> Neutrino physics experiment

MiniBooNE is a Cherenkov detector experiment at Fermilab designed to observe neutrino oscillations. A neutrino beam consisting primarily of muon neutrinos is directed at a detector filled with 800 tons of mineral oil and lined with 1,280 photomultiplier tubes. An excess of electron neutrino events in the detector would support the neutrino oscillation interpretation of the LSND result.

<span class="mw-page-title-main">Gravitational interaction of antimatter</span> Theory of gravity on antimatter

The gravitational interaction of antimatter with matter or antimatter has not been observed by physicists. While the consensus among physicists is that gravity is expected to attract both matter and antimatter at the same rate that matter attracts matter, this is not experimentally confirmed.

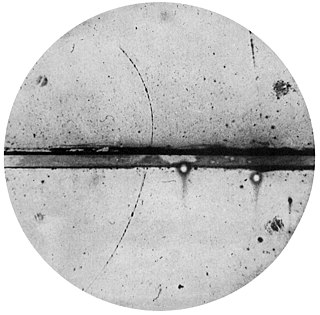
The PS210 experiment was the first experiment that led to the observation of antihydrogen atoms produced at the Low Energy Antiproton Ring (LEAR) at CERN in 1995. The antihydrogen atoms were produced in flight and moved at nearly the speed of light. They made unique electrical signals in detectors that destroyed them almost immediately after they formed by matter–antimatter annihilation.

Gerald Gabrielse is an American physicist. He is the Board of Trustees Professor of Physics and Director of the Center for Fundamental Physics at Northwestern University, and Emeritus George Vasmer Leverett Professor of Physics at Harvard University. He is primarily known for his experiments trapping and investigating antimatter, measuring the electron g-factor, and measuring the electron electric dipole moment. He has been described as "a leader in super-precise measurements of fundamental particles and the study of anti-matter."

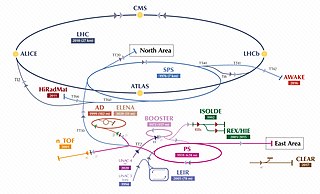
<span class="mw-page-title-main">Antiproton Decelerator</span> Particle storage ring at CERN, Switzerland

The Antiproton Decelerator (AD) is a storage ring at the CERN laboratory near Geneva. It was built from the Antiproton Collector (AC) to be a successor to the Low Energy Antiproton Ring (LEAR) and started operation in the year 2000. Antiprotons are created by impinging a proton beam from the Proton Synchrotron on a metal target. The AD decelerates the resultant antiprotons to an energy of 5.3 MeV, which are then ejected to one of several connected experiments.

<span class="mw-page-title-main">CP violation</span> Violation of charge-parity symmetry in particle physics and cosmology

In particle physics, CP violation is a violation of CP-symmetry : the combination of C-symmetry and P-symmetry. CP-symmetry states that the laws of physics should be the same if a particle is interchanged with its antiparticle (C-symmetry) while its spatial coordinates are inverted. The discovery of CP violation in 1964 in the decays of neutral kaons resulted in the Nobel Prize in Physics in 1980 for its discoverers James Cronin and Val Fitch.

Standard-Model Extension (SME) is an effective field theory that contains the Standard Model, general relativity, and all possible operators that break Lorentz symmetry. Violations of this fundamental symmetry can be studied within this general framework. CPT violation implies the breaking of Lorentz symmetry, and the SME includes operators that both break and preserve CPT symmetry.

Lorentz-violating neutrino oscillation refers to the quantum phenomenon of neutrino oscillations described in a framework that allows the breakdown of Lorentz invariance. Today, neutrino oscillation or change of one type of neutrino into another is an experimentally verified fact; however, the details of the underlying theory responsible for these processes remain an open issue and an active field of study. The conventional model of neutrino oscillations assumes that neutrinos are massive, which provides a successful description of a wide variety of experiments; however, there are a few oscillation signals that cannot be accommodated within this model, which motivates the study of other descriptions. In a theory with Lorentz violation, neutrinos can oscillate with and without masses and many other novel effects described below appear. The generalization of the theory by incorporating Lorentz violation has shown to provide alternative scenarios to explain all the established experimental data through the construction of global models.

<span class="mw-page-title-main">Hughes–Drever experiment</span>

Hughes–Drever experiments are spectroscopic tests of the isotropy of mass and space. Although originally conceived of as a test of Mach's principle, they are now understood to be an important test of Lorentz invariance. As in Michelson–Morley experiments, the existence of a preferred frame of reference or other deviations from Lorentz invariance can be tested, which also affects the validity of the equivalence principle. Thus these experiments concern fundamental aspects of both special and general relativity. Unlike Michelson–Morley type experiments, Hughes–Drever experiments test the isotropy of the interactions of matter itself, that is, of protons, neutrons, and electrons. The accuracy achieved makes this kind of experiment one of the most accurate confirmations of relativity .

<span class="mw-page-title-main">Modern searches for Lorentz violation</span> Overview about the modern searches for Lorentz violation

Modern searches for Lorentz violation are scientific studies that look for deviations from Lorentz invariance or symmetry, a set of fundamental frameworks that underpin modern science and fundamental physics in particular. These studies try to determine whether violations or exceptions might exist for well-known physical laws such as special relativity and CPT symmetry, as predicted by some variations of quantum gravity, string theory, and some alternatives to general relativity.

Searches for Lorentz violation involving photons provide one possible test of relativity. Examples range from modern versions of the classic Michelson–Morley experiment that utilize highly stable electromagnetic resonant cavities to searches for tiny deviations from c in the speed of light emitted by distant astrophysical sources. Due to the extreme distances involved, astrophysical studies have achieved sensitivities on the order of parts in 1038.

<span class="mw-page-title-main">ALPHA experiment</span> Experiment at the Antiproton Decelerator

The Antihydrogen Laser Physics Apparatus (ALPHA), also known as AD-5, is an experiment at the Antiproton Decelerator at CERN, designed to trap neutral antihydrogen in a magnetic trap, and conduct experiments on them. The ultimate goal of this experiment is to test CPT symmetry through comparison of the atomic spectra of hydrogen and antihydrogen. The ALPHA collaboration consists of some former members of the ATHENA collaboration or AD-1 experiment, as well as a number of new members.

The rotating wall technique is a method used to compress a single-component plasma confined in an electromagnetic trap. It is one of many scientific and technological applications that rely on storing charged particles in vacuum. This technique has found extensive use in improving the quality of these traps and in tailoring of both positron and antiproton plasmas for a variety of end uses.

<span class="mw-page-title-main">Penning–Malmberg trap</span> Electromagnetic device used to confine particles of a single sign of charge

The Penning–Malmberg trap, named after Frans Penning and John Malmberg, is an electromagnetic device used to confine large numbers of charged particles of a single sign of charge. Much interest in Penning–Malmberg (PM) traps arises from the fact that if the density of particles is large and the temperature is low, the gas will become a single-component plasma. While confinement of electrically neutral plasmas is generally difficult, single-species plasmas can be confined for long times in PM traps. They are the method of choice to study a variety of plasma phenomena. They are also widely used to confine antiparticles such as positrons and antiprotons for use in studies of the properties of antimatter and interactions of antiparticles with matter.

References

  1. ↑ Colladay, D.; Kostelecky, V.A. (1997). "CPT Violation and the Standard Model". Physical Review D. 55 (11): 6760–6774. arXiv: hep-ph/9703464 . Bibcode:1997PhRvD..55.6760C. doi:10.1103/PhysRevD.55.6760. S2CID   7651433.
  2. ↑ Colladay, D.; Kostelecky, V.A. (1998). "Lorentz-Violating Extension of the Standard Model". Physical Review D. 58 (11): 116002. arXiv: hep-ph/9809521 . Bibcode:1998PhRvD..58k6002C. doi:10.1103/PhysRevD.58.116002. S2CID   4013391.
  3. ↑ Kostelecky, V.A. (2004). "Gravity, Lorentz Violation, and the Standard Model". Physical Review D. 69 (10): 105009. arXiv: hep-th/0312310 . Bibcode:2004PhRvD..69j5009K. doi:10.1103/PhysRevD.69.105009. S2CID   55185765.
  4. ↑ Bluhm, R.; Kostelecky, V.A.; Russell, N. (1997). "Testing CPT with Anomalous Magnetic Moments". Physical Review Letters. 79 (8): 1432–1435. arXiv: hep-ph/9707364 . Bibcode:1997PhRvL..79.1432B. doi:10.1103/PhysRevLett.79.1432. S2CID   119048753.
  5. ↑ Bluhm, R.; Kostelecky, V.A.; Russell, N. (1998). "CPT and Lorentz Tests in Penning Traps". Physical Review D. 57 (7): 3932–3943. arXiv: hep-ph/9809543 . Bibcode:1998PhRvD..57.3932B. doi:10.1103/PhysRevD.57.3932. S2CID   958994.
  6. ↑ Gabrielse, G.; Khabbaz, A.; Hall, D. S.; Heimann, C.; Kalinowsky, H.; Jhe, W. (19 April 1999). "Precision Mass Spectroscopy of the Antiproton and Proton Using Simultaneously Trapped Particles". Physical Review Letters. American Physical Society (APS). 82 (16): 3198–3201. Bibcode:1999PhRvL..82.3198G. doi:10.1103/physrevlett.82.3198. ISSN   0031-9007.
  7. ↑ Mittleman, R. K.; Ioannou, I. I.; Dehmelt, H. G.; Russell, Neil (13 September 1999). "Bound onCPTand Lorentz Symmetry with a Trapped Electron". Physical Review Letters. American Physical Society (APS). 83 (11): 2116–2119. Bibcode:1999PhRvL..83.2116M. doi:10.1103/physrevlett.83.2116. ISSN   0031-9007.
  8. ↑ Dehmelt, H.; Mittleman, R.; Van Dyck, R. S.; Schwinberg, P. (6 December 1999). "Past Electron-Positrong−2Experiments Yielded Sharpest Bound onCPTViolation for Point Particles". Physical Review Letters. 83 (23): 4694–4696. arXiv: hep-ph/9906262 . Bibcode:1999PhRvL..83.4694D. doi:10.1103/physrevlett.83.4694. ISSN   0031-9007. S2CID   116195114.
  9. ↑ Bluhm, R.; Kostelecky, V.A.; Russell, N. (1999). "CPT and Lorentz Tests in Hydrogen and Antihydrogen". Physical Review Letters. 82 (11): 2254–2257. arXiv: hep-ph/9810269 . Bibcode:1999PhRvL..82.2254B. doi:10.1103/PhysRevLett.82.2254. S2CID   10398057.
  10. ↑ Adamson, Allan (19 October 2017). "Universe Should Not Actually Exist: Big Bang Produced Equal Amounts Of Matter And Antimatter". TechTimes.com. Retrieved 26 October 2017.
  11. ↑ Smorra C.; et al. (20 October 2017). "A parts-per-billion measurement of the antiproton magnetic moment". Nature . 550 (7676): 371–374. Bibcode:2017Natur.550..371S. doi: 10.1038/nature24048 . PMID   29052625.
  12. ↑ Bluhm, R.; Kostelecky, V.A.; Lane, C. (2000). "CPT and Lorentz Tests with Muons". Physical Review Letters. 84 (6): 1098–1101. arXiv: hep-ph/9912451 . Bibcode:2000PhRvL..84.1098B. doi:10.1103/PhysRevLett.84.1098. PMID   11017453. S2CID   11593326.
  13. ↑ V.W. Hughes; et al. (2001). "Test of CPT and Lorentz Invariance from Muonium Spectroscopy, Phys. Rev. Lett. 87, 111804 (2001)".{{cite journal}}: Cite journal requires |journal= (help)
  14. ↑ G.W. Bennett; et al. (BNL g-2 collaboration) (2008). "Search for Lorentz and CPT Violation Effects in Muon Spin Precession". Physical Review Letters. 100 (9): 091602. arXiv: 0709.4670 . Bibcode:2008PhRvL.100i1602B. doi:10.1103/PhysRevLett.100.091602. PMID   18352695. S2CID   26270066.
  15. ↑ Kostelecky, V.A.; Russell, N. (2010). "Data Tables for Lorentz and CPT Violation". Reviews of Modern Physics. 83 (1): 11–31. arXiv: 0801.0287 . Bibcode:2011RvMP...83...11K. doi:10.1103/RevModPhys.83.11. S2CID   3236027.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.